题目内容
9.执行如图所示的程序框图,输出的a,b的值分别等于( )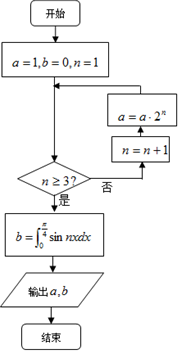
| A. | 32,$-\frac{{\sqrt{2}}}{6}-\frac{1}{3}$ | B. | 32,$\frac{{\sqrt{2}}}{6}+\frac{1}{3}$ | C. | 8,$-\frac{{\sqrt{2}}}{2}-1$ | D. | 32,$\frac{{\sqrt{2}}}{2}+1$ |
分析 模拟程序的运行过程,分析循环中各变量值的变化情况,可得a的值,进而由定积分可求b,从而得解.
解答 解:模拟程序的运行,可得:
a=1,b=0,n=1
不满足条件n≥3,执行循环体,n=2,a=4;
不满足条件n≥3,执行循环体,n=3,a=4×23=32;
满足条件n≥3,退出循环,可得:$a=32,b=\int_0^{\frac{π}{4}}{sin3xdx}=(-\frac{1}{3}cos3x)|_0^{\frac{π}{4}}=\frac{{\sqrt{2}}}{6}+\frac{1}{3}$,
所以输出a,b的值分别等于32,$\frac{{\sqrt{2}}}{6}+\frac{1}{3}$.
故选:B.
点评 本题考查了程序框图的应用问题,解题时应模拟程序框图的运行过程,以便得出正确的结论,是基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
4.运行如下程序框图,如果输入的t∈[0,5],则输出S属于( )
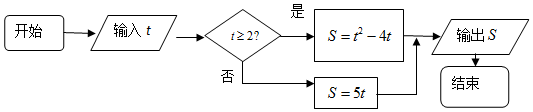

| A. | [-4,10) | B. | [-5,2] | C. | [-4,3] | D. | [-2,5] |
18.定义运算:$|\begin{array}{l}{{a}_{1}}&{{a}_{2}}\\{{a}_{3}}&{{a}_{4}}\end{array}|$=a1a4-a2a3,将函数f(x)=$|\begin{array}{l}{\sqrt{3}}&{sinωx}\\{1}&{cosωx}\end{array}|$(ω>0)的图象向左平移$\frac{2π}{3}$个单位,所得图象对应的函数为奇函数,则ω的最小值是( )
| A. | $\frac{1}{2}$ | B. | $\frac{5}{4}$ | C. | 2 | D. | $\frac{3}{4}$ |
3.已知以O为中心的双曲线C的一个焦点为F,P为C上一点,M为PF的中点,若△OMF为等腰直角三角形,则C的离心率等于( )
| A. | $\sqrt{2}-1$ | B. | $\sqrt{2}+1$ | C. | $2+\sqrt{2}$ | D. | $\frac{\sqrt{5}+1}{2}$ |
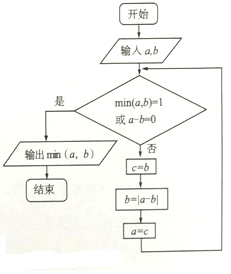 min(a,b)表示a,b中的最小值,执行如图所示的程序框图,若输入的a,b值分别为4,10,则输出的min(a,b)值是( )
min(a,b)表示a,b中的最小值,执行如图所示的程序框图,若输入的a,b值分别为4,10,则输出的min(a,b)值是( )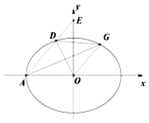 如图,在平面直角坐标系xOy中,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左顶点为A(-2,0),离心率为$\frac{\sqrt{2}}{2}$,过A作斜率为k(k≠0)的直线l交椭圆C于点D,交y轴为E,过点O作直线l的平行线交椭圆于点G,设△AOD,△AOE,△DOG的面积分别为S1、S2、S3.
如图,在平面直角坐标系xOy中,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左顶点为A(-2,0),离心率为$\frac{\sqrt{2}}{2}$,过A作斜率为k(k≠0)的直线l交椭圆C于点D,交y轴为E,过点O作直线l的平行线交椭圆于点G,设△AOD,△AOE,△DOG的面积分别为S1、S2、S3.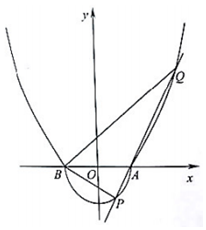 如图,由半圆x2+y2=r2(y≤0,r>0)和部分抛物线y=a(x2-1)(y≥0,a>0)合成的曲线C称为“羽毛球形线”,曲线C与x轴有A、B两个焦点,且经过点(2.3).
如图,由半圆x2+y2=r2(y≤0,r>0)和部分抛物线y=a(x2-1)(y≥0,a>0)合成的曲线C称为“羽毛球形线”,曲线C与x轴有A、B两个焦点,且经过点(2.3).