题目内容
14．已知${（{\frac{3}{{\sqrt{a}}}-\root{3}{a}}）^n}$的展开式的各项系数之和等于${（{4\root{3}{b}-\frac{1}{{\sqrt{5b}}}}）^5}$展开式中的常数项，求${（{\frac{3}{{\sqrt{a}}}-\root{3}{a}}）^n}$展开式中含$\frac{1}{a}$的项的二项式系数．分析 令a=1求得${（{\frac{3}{{\sqrt{a}}}-\root{3}{a}}）^n}$的展开式的各项系数之和，
由二项展开式的通项公式求得${（{4\root{3}{b}-\frac{1}{{\sqrt{5b}}}}）^5}$展开式中的常数项，
从而求得n的值，再计算${（{\frac{3}{{\sqrt{a}}}-\root{3}{a}}）^7}$展开式中$含\frac{1}{a}$项的二项式系数．
解答 解：令a=1得${（{\frac{3}{{\sqrt{a}}}-\root{3}{a}}）^n}$的展开式的各项系数之和为2n，…（2分）
由二项展开式的通项公式得
${T_{r+1}}=C_5^r{（4\root{3}{b}）^{5-r}}{（-\frac{1}{{\sqrt{5b}}}）^r}=C_5^r{4^{5-r}}{（-\frac{1}{{\sqrt{5}}}）^r}b_{\;}^{\frac{10-5r}{6}}$，
令10-5r=0，解得r=2，…（4分）
所以${（{4\root{3}{b}-\frac{1}{{\sqrt{5b}}}}）^5}$的展开式中的常数项是第3项，
即${T_3}=C_5^2{4^3}{（-\frac{1}{{\sqrt{5}}}）^2}={2^7}$，
由2n=27得n=7；…（8分）
对于${（{\frac{3}{{\sqrt{a}}}-\root{3}{a}}）^7}$，由二项展开式的通项公式得
${T_{r+1}}=C_7^r{（\frac{3}{{\sqrt{a}}}）^{7-r}}{（-\root{3}{a}）^r}={（-1）^r}C_7^r{3^{7-r}}a_{\;}^{\frac{5r-21}{6}}$，
所以$含\frac{1}{a}$的项是第4项，其二项式系数是$C_7^3=35$．…（12分）
点评 本题考查了二项式定理的应用问题，也考查了二项式系数与常数项的应用问题，是中档题．
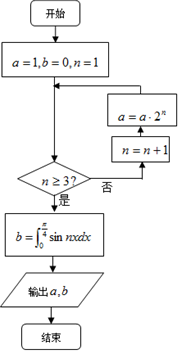
| A． | 32，$-\frac{{\sqrt{2}}}{6}-\frac{1}{3}$ | B． | 32，$\frac{{\sqrt{2}}}{6}+\frac{1}{3}$ | C． | 8，$-\frac{{\sqrt{2}}}{2}-1$ | D． | 32，$\frac{{\sqrt{2}}}{2}+1$ |
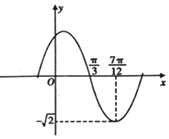函数f（x）=Asin（ωx+φ），（A，ω，φ是常数，A＞0，ω＞0，|φ|≤$\frac{π}{2}$）的部分图象如图所示，则y=f（x）在x∈[-$\frac{π}{4}$，$\frac{π}{2}$]上的取值范围是（ ）| A． | [-$\frac{\sqrt{2}}{2}$，$\sqrt{2}$] | B． | [$\frac{\sqrt{2}}{2}$，$\sqrt{2}$] | C． | [-$\frac{\sqrt{6}}{2}$，$\sqrt{2}$] | D． | [$\frac{\sqrt{6}}{2}$，$\sqrt{2}$] |
某职称晋级评定机构对参加某次专业技术考试的100人的成绩进行了统计，绘制了频率分布直方图（如图所示），规定80分及以上者晋级成功，否则晋级失败．| 晋级成功 | 晋级失败 | 合计 | |
| 男 | 16 | ||
| 女 | 50 | ||
| 合计 |
（Ⅱ）根据已知条件完成下面2×2列联表，并判断能否有85%的把握认为“晋级成功”与性别有关？
（Ⅲ）将频率视为概率，从本次考试的所有人员中，随机抽取4人进行约谈，记这4人中晋级失败的人数为X，求X的分布列与数学期望E（X）．
（参考公式：${k^2}=\frac{{n{{（ad-bc）}^2}}}{（a+b）（c+d）（a+c）（b+d）}$，其中n=a+b+c+d）
| P（K2≥k0） | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| k0 | 0.780 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |