题目内容
7．已知二项式${（\root{3}{x^2}+\frac{1}{x}）^n}$的展开式中含有x2的项是第3项，则n=8．分析 首先写出展开式的通项，由题意得到关于n 的等式解之．
解答 解：二项式${（\root{3}{x^2}+\frac{1}{x}）^n}$的展开式中通项为${T}_{r+1}={C}_{n}^{r}（\root{3}{{x}^{2}}）^{n-r}（\frac{1}{x}）^{r}$=${C}_{n}^{r}{x}^{\frac{2n-5r}{3}}$，
因为展开式中含有x2的项是第3项，所以r=2时2n-5r=6，解得n=8；
故答案为：8．
点评 本题考查了二项式定理的运用；熟练掌握展开式的通项是解答的关键．
练习册系列答案
相关题目
18．已知△ABC中，AC=$\sqrt{2}，BC=\sqrt{6}$，∠ACB=$\frac{π}{6}$，若线段BA的延长线上存在点D，使∠BDC=$\frac{π}{4}$，则CD=（ ）
| A． | $\sqrt{2}$ | B． | $\sqrt{3}$ | C． | 3 | D． | $2\sqrt{3}$ |
15．
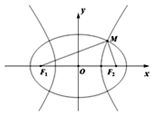已知椭圆C1：$\frac{{x}^{2}}{{m}^{2}}$+$\frac{{y}^{2}}{{p}^{2}}$=1（m＞p＞0）与双曲线C2：$\frac{{x}^{2}}{{n}^{2}}$-$\frac{{y}^{2}}{{p}^{2}}$=1（n＞0）有公共的焦点F1，F2，设M为C1与C2在第一象限内的交点，|F1F2|=2c．则（ ）
已知椭圆C1：$\frac{{x}^{2}}{{m}^{2}}$+$\frac{{y}^{2}}{{p}^{2}}$=1（m＞p＞0）与双曲线C2：$\frac{{x}^{2}}{{n}^{2}}$-$\frac{{y}^{2}}{{p}^{2}}$=1（n＞0）有公共的焦点F1，F2，设M为C1与C2在第一象限内的交点，|F1F2|=2c．则（ ）| A． | m2+n2=2c2，且∠F1MF2＞$\frac{π}{2}$ | B． | m2+n2=2c2，且∠F1MF2=$\frac{π}{2}$ | ||
| C． | m2+n2=4c2，且∠F1MF2＞$\frac{π}{2}$ | D． | m2+n2=4c2，且∠F1MF2=$\frac{π}{2}$ |
12．已知{an}是公差为2的等差数列，若a1，a3，a4成等比数列，则a2=（ ）
| A． | -4 | B． | -8 | C． | -10 | D． | -6 |
19．
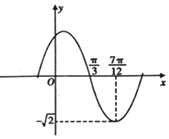函数f（x）=Asin（ωx+φ），（A，ω，φ是常数，A＞0，ω＞0，|φ|≤$\frac{π}{2}$）的部分图象如图所示，则y=f（x）在x∈[-$\frac{π}{4}$，$\frac{π}{2}$]上的取值范围是（ ）
函数f（x）=Asin（ωx+φ），（A，ω，φ是常数，A＞0，ω＞0，|φ|≤$\frac{π}{2}$）的部分图象如图所示，则y=f（x）在x∈[-$\frac{π}{4}$，$\frac{π}{2}$]上的取值范围是（ ）| A． | [-$\frac{\sqrt{2}}{2}$，$\sqrt{2}$] | B． | [$\frac{\sqrt{2}}{2}$，$\sqrt{2}$] | C． | [-$\frac{\sqrt{6}}{2}$，$\sqrt{2}$] | D． | [$\frac{\sqrt{6}}{2}$，$\sqrt{2}$] |