题目内容
5.已知直线l1:x-2y=0的倾斜角为α,倾斜角为2α的直线l2与圆M:x2+y2+2x-2y+F=0交于A、C两点,其中A(-1,0)、B、D在圆M上,且位于直线l2的两侧,则四边形ABCD的面积的最大值是$\frac{8}{5}$.分析 由已知求出tanα,得到直线l2的斜率,进一步求得方程,由A在圆上求得F,得到圆的方程,求出圆心坐标和半径,利用垂径定理求得|AC|的长度,然后结合圆与直线的位置关系图象,将ABCD的面积看成两个三角形△ABC和△ACD的面积之和,分析可得当BD为AC的垂直平分线时,四边形ABCD的面积最大.
解答 解:直线l1:x-2y=0的倾斜角为α,则tanα=$\frac{1}{2}$,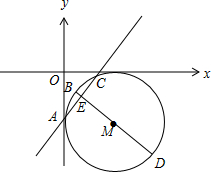
∴直线l2的斜率k=tan2α=$\frac{2tanα}{1-ta{n}^{2}α}=\frac{2×\frac{1}{2}}{1-\frac{1}{4}}=\frac{4}{3}$.
则直线l2的方程为y-0=$\frac{4}{3}$(x+1),即4x-3y+4=0.
又A(-1,0)在圆上,∴(-1)2-2+F=0,得F=1,
∴圆的方程为x2+y2+2x-2y+1=0,化为标准方程:(x+1)2+(y-1)2=1,圆心(-1,1),半径r=1.
直线l2与圆M相交于A,C两点,由点到直线的距离公式得弦心距d=$\frac{|4×(-1)-3×1+4|}{\sqrt{{4}^{2}+(-3)^{2}}}=\frac{3}{5}$,
由勾股定理得半弦长=$\sqrt{{1}^{2}-(\frac{3}{5})^{2}}=\frac{4}{5}$,
弦长|AC|=2×$\frac{4}{5}$=$\frac{8}{5}$.
又B,D两点在圆上,并且位于直线l2的两侧,四边形ABCD的面积可以看成是两个三角形△ABC和△ACD的面积之和,
如图所示,
当BD为弦AC的垂直平分线时(即为直径时),两三角形的面积之和最大,即四边形ABCD的面积最大,
最大面积为:S=$\frac{1}{2}$|AC|×|BE|+$\frac{1}{2}$|AC|×|DE|=$\frac{1}{2}$|AC|×|BD|=$\frac{1}{2}$×$\frac{8}{5}$×2=$\frac{8}{5}$,
故答案为:$\frac{8}{5}$.
点评 本题考查直线与圆位置关系的应用,考查数形结合的解题思想方法,属于中档题.

 巧学巧练系列答案
巧学巧练系列答案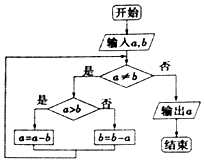
| A. | 1 | B. | 2 | C. | 4 | D. | 12 |
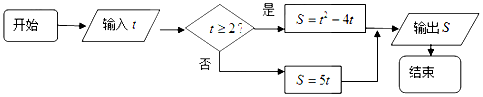
| A. | 10 | B. | 5 | C. | 0 | D. | -5 |
附:若随机变量ξ服从正态分布N(μ,σ2),则P(μ-σ<ξ<μ+σ)=0.6826,P(μ-2σ<ξ<μ+2σ)=0.9544.
| A. | 0.2718 | B. | 0.0456 | C. | 0.3174 | D. | 0.1359 |
| A. | $\frac{3}{4}$ | B. | $\frac{3}{5}$ | C. | $\frac{1}{2}$ | D. | $\frac{5}{9}$ |