12.已知两点M(-1,0),N(1,0),若直线y=k(x-2)上至少存在三个点P,使得△MNP是直角三角形,则实数k的取值范围是( )
| A. | $[-\frac{{\sqrt{3}}}{3}\;\;,\;\frac{{\sqrt{3}}}{3}]$ | B. | $[-\frac{1}{3}\;,\;\frac{1}{3}]$ | C. | $[-\frac{1}{3}\;,\;0)∪(0\;,\;\frac{1}{3}]$ | D. | $[-\frac{{\sqrt{3}}}{3}\;,\;0)∪(0\;,\;\frac{{\sqrt{3}}}{3}]$ |
11.下列说法正确的是( )
| A. | 若|$\vec a|>|\vec b|$,$\vec a>\vec b$ | B. | 若$|\vec a|=|\vec b|$,$\vec a=\vec b$ | ||
| C. | 若$\vec a=\vec b$,则$\vec a∥\vec b$ | D. | 若$\vec a≠\vec b$,则$\vec a$与$\vec b$不是共线向量 |
10.在△ABC中,AB=3,AC=2,∠BAC=60°,点P是△ABC内一点(含边界),若$\overrightarrow{AP}=\frac{2}{3}\overrightarrow{AB}+λ\overrightarrow{AC}$,则|$\overrightarrow{AP}$|的最大值为( )
| A. | $\frac{2\sqrt{7}}{3}$ | B. | $\frac{8}{3}$ | C. | $\frac{2\sqrt{19}}{3}$ | D. | $\frac{2\sqrt{13}}{3}$ |
9.设等差数列{an}的前n项和为Sn,若a4,a6是方程x2-18x+p=0的两根,那么S9=( )
0 239740 239748 239754 239758 239764 239766 239770 239776 239778 239784 239790 239794 239796 239800 239806 239808 239814 239818 239820 239824 239826 239830 239832 239834 239835 239836 239838 239839 239840 239842 239844 239848 239850 239854 239856 239860 239866 239868 239874 239878 239880 239884 239890 239896 239898 239904 239908 239910 239916 239920 239926 239934 266669
| A. | 9 | B. | 81 | C. | 5 | D. | 45 |
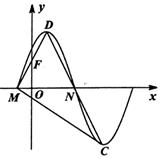 如图是函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<$\frac{π}{2}$)的部分图象,M,N是它与x轴的两个交点,D,C分别为它的最高点和最低点,点F(0,1)是线段MD的中点,三角形MDC的面积为$\frac{2π}{3}$.
如图是函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<$\frac{π}{2}$)的部分图象,M,N是它与x轴的两个交点,D,C分别为它的最高点和最低点,点F(0,1)是线段MD的中点,三角形MDC的面积为$\frac{2π}{3}$.