题目内容
9.设等差数列{an}的前n项和为Sn,若a4,a6是方程x2-18x+p=0的两根,那么S9=( )| A. | 9 | B. | 81 | C. | 5 | D. | 45 |
分析 利用韦达定理求出a4+a6=18,再由等差数列通项公式和前n项和公式得S9=$\frac{9}{2}({a}_{1}+{a}_{9})$=$\frac{9}{2}$(a4+a6),由此能求出结果.
解答 解:∵等差数列{an}的前n项和为Sn,
a4,a6是方程x2-18x+p=0的两根,那
∴a4+a6=18,
∴S9=$\frac{9}{2}({a}_{1}+{a}_{9})$=$\frac{9}{2}({a}_{4}+{a}_{6})=\frac{9}{2}×18$=81.
故选:B.
点评 本题考查等差数列的前9项和的求法,涉及到韦达定理、等差数列等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想,是基础题.

练习册系列答案
 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
4.已知$a={log_2}3,b={2^{-\frac{1}{3}}},c={log_{\frac{1}{3}}}\frac{1}{30}$,则a、b、c的大小关系是( )
| A. | c>a>b | B. | a>c>b | C. | a>b>c | D. | c>b>a |
1.把8个相同的小球全部放入编号为1,2,3,4的四个盒中,则不同的放法数为( )
| A. | 35 | B. | 70 | C. | 165 | D. | 1860 |
18.设曲线y=ex-x及直线y=0所围成的图形为区域D,不等式组$\left\{\begin{array}{l}-1≤x≤1\\ 0≤y≤2\end{array}\right.$所确定的区域为E,在区域E内随机取一点,则该点落在区域D内的概率为( )
| A. | $\frac{{{e^2}-2e-1}}{4e}$ | B. | $\frac{{{e^2}-2e}}{4e}$ | C. | $\frac{{{e^2}-e-1}}{4e}$ | D. | $\frac{{{e^2}-1}}{4e}$ |
19.某人午觉醒来,发现表停了,他打开收音机,想听电台报时,则他等待时间大于10分钟的概率为( )
| A. | $\frac{1}{6}$ | B. | $\frac{5}{6}$ | C. | $\frac{1}{10}$ | D. | $\frac{9}{10}$ |
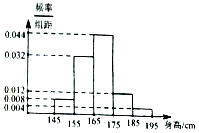 某校共有学生1800人,现从中随机抽取一个50人的样本,以估计该校学生的身体状况,测得样本身高小于195cm的频率分布直方图如图,由此估计该校身高不小于175的人数是288.
某校共有学生1800人,现从中随机抽取一个50人的样本,以估计该校学生的身体状况,测得样本身高小于195cm的频率分布直方图如图,由此估计该校身高不小于175的人数是288.