题目内容
12.已知两点M(-1,0),N(1,0),若直线y=k(x-2)上至少存在三个点P,使得△MNP是直角三角形,则实数k的取值范围是( )| A. | $[-\frac{{\sqrt{3}}}{3}\;\;,\;\frac{{\sqrt{3}}}{3}]$ | B. | $[-\frac{1}{3}\;,\;\frac{1}{3}]$ | C. | $[-\frac{1}{3}\;,\;0)∪(0\;,\;\frac{1}{3}]$ | D. | $[-\frac{{\sqrt{3}}}{3}\;,\;0)∪(0\;,\;\frac{{\sqrt{3}}}{3}]$ |
分析 若直线y=k(x-2)上至少存在三个点P,使得△MNP是直角三角形,则此直线与以MN为直径的圆必须有公共点,但是去掉x轴.
解答 解:若直线y=k(x-2)上至少存在三个点P,使得△MNP是直角三角形,
则此直线与以MN为直径的圆必须有公共点,但是去掉x轴.
∴$\frac{|2k|}{\sqrt{1+{k}^{2}}}$≤1,k≠0,化为:0<k2$≤\frac{1}{3}$.
解得$-\frac{\sqrt{3}}{3}$≤k$≤\frac{\sqrt{3}}{3}$,且k≠0.
故选:D.
点评 本题考查了直线与圆的位置关系、点到直线的距离公式、方程与不等式的解法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
1.在等比数列{an}中,已知a4=8a1,且a1,a2+1,a3成等差数列.则{an}的前5项和为( )
| A. | 31 | B. | 62 | C. | 64 | D. | 128 |
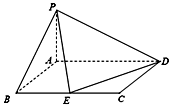 如图,PA⊥平面ABCD,矩形ABCD的边长AB=1,BC=2,E为BC的中点.
如图,PA⊥平面ABCD,矩形ABCD的边长AB=1,BC=2,E为BC的中点.