题目内容
14.用“五点法”画y=2sin(2x+$\frac{π}{3}$)在一个周期内的简图时,所描的五个点分别是($-\frac{π}{6}$,0),($\frac{π}{12}$,2),($\frac{π}{3}$,0),($\frac{7π}{12}$,-2),($\frac{5π}{6}$,0).分析 令2x+$\frac{π}{3}$=2π,即可求出最后一个关键点.
解答 解:令2x+$\frac{π}{3}$=2π,则解得x=$\frac{5π}{6}$,
可得:最后一个关键点是($\frac{5π}{6}$,0).
故答案为:($\frac{5π}{6}$,0).
点评 本题考查三角函数图象的画法,考查学生的计算能力,属于基础题.

练习册系列答案
相关题目
9.设等差数列{an}的前n项和为Sn,若a4,a6是方程x2-18x+p=0的两根,那么S9=( )
| A. | 9 | B. | 81 | C. | 5 | D. | 45 |
19.已知i是虚数单位,复数$\frac{z}{2-3i}$对应于复平面内一点(0,1),则|z|=( )
| A. | $\sqrt{13}$ | B. | 4 | C. | 5 | D. | $4\sqrt{2}$ |
4.已知点P在双曲线$\frac{x^2}{16}-\frac{y^2}{9}=1$上,点A满足$\overrightarrow{PA}=(t-1)\overrightarrow{OP}$(t∈R),且$\overrightarrow{OA}•\overrightarrow{OP}=64$,$\overrightarrow{OB}=(0,1)$,则$|{\overrightarrow{OB}•\overrightarrow{OA}}|$的最大值为( )
| A. | $\frac{5}{4}$ | B. | $\frac{24}{5}$ | C. | $\frac{4}{5}$ | D. | $\frac{5}{24}$ |
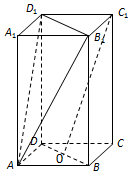 如图,长方体ABCD-A1B1C1D1中,O是BD的中点,AA1=2AB=2BC=4.
如图,长方体ABCD-A1B1C1D1中,O是BD的中点,AA1=2AB=2BC=4.