题目内容
13.已知定义域为R的函数f(x)既是奇函数,又是周期为3的周期函数,当x∈(0,$\frac{3}{2}$)时,f(x)=sinπx,f($\frac{3}{2}$)=0,则函数f(x)在区间[0,6]上的零点个数是( )| A. | 3 | B. | 5 | C. | 7 | D. | 9 |
分析 利用周期和对称性作出f(x)的函数图象,根据图象判断零点个数.
解答 解:作出f(x)的函数图象如图所示:
由图象可知f(x)在区间[0,6]上共有9个零点,
故选:D.
点评 本题考查了函数的奇偶性与周期性的应用,函数零点与函数图象的关系,属于中档题.

练习册系列答案
相关题目
3.2016年上半年数据显示,某市空气质量在其所在省中排名倒数第三,PM10(可吸入颗粒物)和PM2.5(细颗粒物)分别排在倒数第一和倒数第四,这引起有关部门高度重视,该市采取一系列“组合拳”治理大气污染,计划到2016年底,全年优、良天数达到190天.下表是2016年9月1日到9月15日该市的空气质量指数(AQI),其中空气质量指数划分为0~50,51~100,101~150,151~200,201~300和大于300六档,对应空气质量依次为优、良、轻度污染、中度污染、重度污染、严重污染.
(1)指出这15天中PM2.5的最大值及PM10的最大值;
(2)从这15天中连续取2天,求这2天空气质量均为优、良的概率;
(3)已知2016年前8个月(每个月按30天计算)该市空气质量为优、良的天数约占55%,用9月份这15天空气质量优、良的频率作为2016年后4个月空气质量优、良的概率(不考虑其他因素),估计该市到2016年底,能否完成全年优、良天数达到190天的目标.
| 日期 | 1日 | 2日 | 3日 | 4日 | 5日 | 6日 | 7日 | 8日 | 9日 | 10日 | 11日 | 12日 | 13日 | 14日 | 15日 |
| AQI指数 | 72 | 74 | 115 | 192 | 138 | 123 | 74 | 80 | 105 | 73 | 91 | 90 | 77 | 109 | 124 |
| PM2.5 | 36 | 29 | 76 | 112 | 89 | 85 | 40 | 32 | 59 | 35 | 45 | 59 | 53 | 79 | 89 |
| PM10 | 76 | 86 | 148 | 199 | 158 | 147 | 70 | 83 | 121 | 75 | 96 | 90 | 63 | 113 | 140 |
(2)从这15天中连续取2天,求这2天空气质量均为优、良的概率;
(3)已知2016年前8个月(每个月按30天计算)该市空气质量为优、良的天数约占55%,用9月份这15天空气质量优、良的频率作为2016年后4个月空气质量优、良的概率(不考虑其他因素),估计该市到2016年底,能否完成全年优、良天数达到190天的目标.
1.设f(x)=cos2x-sin2x,把y=f(x)的图象向右平移φ(φ>0)个单位后,恰好得到函数y=f(x)的图象,则φ的值可以为( )
| A. | $\frac{π}{2}$ | B. | $\frac{3π}{4}$ | C. | π | D. | $\frac{3π}{2}$ |
8.已知函数f(x)是偶函数,f(x+1)是奇函数,且对任意的x1,x2∈[0,1],且x1≠x2,都有(x1-x2)[f(x1)-f(x2)]<0,设a=f($\frac{82}{11}$),b=-f($\frac{50}{9}$),c=f($\frac{24}{7}$),则下列结论正确的是( )
| A. | a>b>c | B. | b>a>c | C. | b>c>a | D. | c>a>b |
5.函数f(x)=sin(ωx+φ)+$\sqrt{3}cos({ωx+φ})({ω>0})$的图象过(1,2),若f(x)相邻的零点为x1,x2且满足|x1-x2|=6,则f(x)的单调增区间为( )
| A. | [-2+12k,4+12k](k∈Z) | B. | [-5+12k,1+12k](k∈Z) | C. | [1+12k,7+12k](k∈Z) | D. | [-2+6k,1+6k](k∈Z) |
3.设集合A={x|x<-2或x>1,x∈R},B={x|x<0或x>2,x∈R},则(∁RA)∩B是( )
| A. | (-2,0) | B. | (-2,0] | C. | [-2,0) | D. | R |
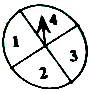 在英国的某一娱乐节目中,有一种过关游戏,规则如下:转动图中转盘(一个圆盘四等分,在每块区域内分别标有数字1,2,3,4),由转盘停止时指针所指数字决定是否过关.在闯n关时,转n次,当次转得数字之和大于n2时,算闯关成功,并继续闯关,否则停止闯关,闯过第一关能获得10欧元,之后每多闯一关,奖金翻倍.假设每个参与者都会持续闯关到不能过关为止,并且转盘每次转出结果相互独立.
在英国的某一娱乐节目中,有一种过关游戏,规则如下:转动图中转盘(一个圆盘四等分,在每块区域内分别标有数字1,2,3,4),由转盘停止时指针所指数字决定是否过关.在闯n关时,转n次,当次转得数字之和大于n2时,算闯关成功,并继续闯关,否则停止闯关,闯过第一关能获得10欧元,之后每多闯一关,奖金翻倍.假设每个参与者都会持续闯关到不能过关为止,并且转盘每次转出结果相互独立.