18.已知x>0,y>0且2x+3y=8,则$\frac{2}{x}+\frac{3}{y}$的最小值为( )
| A. | $\frac{25}{8}$ | B. | $\frac{25}{4}$ | C. | 25 | D. | $\frac{4}{25}$ |
17.通过随机询问100名性别不同的大学生是否爱好踢毽子,得到如右的列联表,经计算,统计量K2的观测值k2≈5.762,参照附表,则所得到的统计学结论为:有( )把握认为“爱好该项运动与性别有关”.
| 男 | 女 | 总计 | |
| 爱好 | 10 | 40 | 50 |
| 不爱好 | 20 | 30 | 50 |
| 总计 | 30 | 70 | 100 |
| A. | 0.25% | B. | 2.5% | C. | 97.5% | D. | 99.75% |
16.a,b,c,d四个人各自对两个变量x,y进行相关性的测试试验,并用回归分析方法分别求得相关指数R2与残差平方和m(如表),则这四位同学中,( )同学的试验结果体现两个变量x,y有更强的相关性.
| a | b | c | d | |
| r | 0.80 | 0.76 | 0.67 | 0.82 |
| m | 100 | 113 | 121 | 99 |
| A. | a | B. | b | C. | c | D. | d |
14.通过随机询问100名性别不同的大学生是否爱好踢毽子,得到如的列联表,参照附表,则在犯错误概率不超过( )情况下认为“爱好该项运动与性别有关”.
| 男 | 女 | 总计 | |
| 爱好 | 10 | 40 | 50 |
| 不爱好 | 20 | 30 | 50 |
| 总计 | 30 | 70 | n |
| A. | 1% | B. | 2.5% | C. | 5% | D. | 10% |
13.从含有4件正品、2件次品的6件产品中,随机抽取3件,则恰好抽到1件次品的概率( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{5}$ |
11.著名数学家华罗庚曾说过:“数形结合百般好,隔裂分家万事休.”事实上,有很多代数问题可以转化为几何问题加以解决,如:$\sqrt{(x-a)^{2}+(y-b)^{2}}$可以转化为平面上点M(x,y)与点N(a,b)的距离.结合上述观点,可得f(x)=$\sqrt{{x}^{2}+4x+20}$+$\sqrt{{x}^{2}+2x+10}$的最小值为( )
0 239472 239480 239486 239490 239496 239498 239502 239508 239510 239516 239522 239526 239528 239532 239538 239540 239546 239550 239552 239556 239558 239562 239564 239566 239567 239568 239570 239571 239572 239574 239576 239580 239582 239586 239588 239592 239598 239600 239606 239610 239612 239616 239622 239628 239630 239636 239640 239642 239648 239652 239658 239666 266669
| A. | $3\sqrt{2}$ | B. | $4\sqrt{2}$ | C. | $5\sqrt{2}$ | D. | $7\sqrt{2}$ |
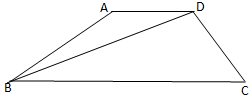 在四边形ABCD中,AD∥BC,AB=$\sqrt{3}$,AD=1,A=$\frac{5π}{6}$
在四边形ABCD中,AD∥BC,AB=$\sqrt{3}$,AD=1,A=$\frac{5π}{6}$