题目内容
14.通过随机询问100名性别不同的大学生是否爱好踢毽子,得到如的列联表,参照附表,则在犯错误概率不超过( )情况下认为“爱好该项运动与性别有关”.| 男 | 女 | 总计 | |
| 爱好 | 10 | 40 | 50 |
| 不爱好 | 20 | 30 | 50 |
| 总计 | 30 | 70 | n |
| A. | 1% | B. | 2.5% | C. | 5% | D. | 10% |
分析 根据题意,由列联表计算可得k2=$\frac{100(10×30-20×40)^{2}}{50×50×30×70}$≈4.762,与临界值对照表比较可得答案.
解答 解:根据题意,n=100,
由列联表可得:k2=$\frac{100(10×30-20×40)^{2}}{50×50×30×70}$≈4.762,
参照对照表,可得在犯错误的概率不超过5%的前提下,认为“爱好这项运动与性别有关”;
故选:C.
点评 本题考查独立性检验的应用,关键是理解独立性检验的思想并正确计算观测值.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
3.函数f(x)=cos(3x+φ)的图象关于原点成中心对称,则φ等于( )
| A. | -$\frac{π}{2}$ | B. | 2kπ-$\frac{π}{2}$(k∈Z) | C. | kπ(k∈Z) | D. | kπ+$\frac{π}{2}$(k∈Z) |
4.函数f(x)=x2-2x-1,x∈[-3,2]的最大值、最小值分别为( )
| A. | 14,-2 | B. | 14,-1 | C. | 2,-2 | D. | 7,-2 |

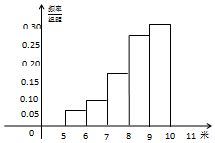 某市为了解今年高中毕业生的身体素质状况,从本市某校高中毕业班中抽取一个班进行实心球测试,成绩在8米及以上的为合格.把所得数据整理后,分成六组得到频率分布直方图的一部分(如图).已知前五个小组的频率分别为0.06.0.10,0.14,0.28,0.30.第六小组的频数是6.
某市为了解今年高中毕业生的身体素质状况,从本市某校高中毕业班中抽取一个班进行实心球测试,成绩在8米及以上的为合格.把所得数据整理后,分成六组得到频率分布直方图的一部分(如图).已知前五个小组的频率分别为0.06.0.10,0.14,0.28,0.30.第六小组的频数是6.