15.在△ABC中,A=60°,b=1,${S_{△ABC}}=\sqrt{3}$,则$\frac{c}{sinC}$=( )
| A. | $\frac{{8\sqrt{3}}}{81}$ | B. | $\frac{{2\sqrt{39}}}{3}$ | C. | $\frac{{26\sqrt{3}}}{3}$ | D. | $2\sqrt{7}$ |
14.若变量x,y满足条件$\left\{\begin{array}{l}x-y-1≤0\\ x+y-6≤0\\ x-1≥0\end{array}\right.$,则xy的取值范围是( )
| A. | [0,5] | B. | $[{5,\frac{35}{4}}]$ | C. | $[{0,\frac{35}{4}}]$ | D. | [0,9] |
13.将函数f(x)的图象向左平移$\frac{π}{6}$个单位后得到函数g(x)的图象如图所示,则函数f(x)的解析式是( )
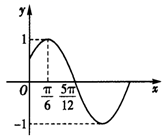

| A. | $f(x)=sin({2x-\frac{π}{6}})$(x∈R) | B. | $f(x)=sin({2x+\frac{π}{6}})$(x∈R) | C. | $f(x)=sin({2x-\frac{π}{3}})$(x∈R) | D. | $f(x)=sin({2x+\frac{π}{3}})$(x∈R) |
12.若二项式${({{x^2}-\frac{2}{x}})^n}$展开式的二项式系数之和为8,则该展开式的系数之和为( )
| A. | -1 | B. | 1 | C. | 27 | D. | -27 |
11.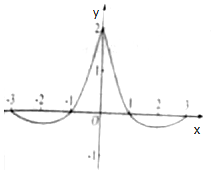 已知函数f(x)=$\frac{{cos({ωx+φ})}}{{a•{e^{|x|}}}}$(ω>0,|φ|<$\frac{π}{2}$,a∈R)在区间[-3,3]上的图象如图所示,则$\frac{ω}{a}$可取( )
已知函数f(x)=$\frac{{cos({ωx+φ})}}{{a•{e^{|x|}}}}$(ω>0,|φ|<$\frac{π}{2}$,a∈R)在区间[-3,3]上的图象如图所示,则$\frac{ω}{a}$可取( )
 已知函数f(x)=$\frac{{cos({ωx+φ})}}{{a•{e^{|x|}}}}$(ω>0,|φ|<$\frac{π}{2}$,a∈R)在区间[-3,3]上的图象如图所示,则$\frac{ω}{a}$可取( )
已知函数f(x)=$\frac{{cos({ωx+φ})}}{{a•{e^{|x|}}}}$(ω>0,|φ|<$\frac{π}{2}$,a∈R)在区间[-3,3]上的图象如图所示,则$\frac{ω}{a}$可取( )| A. | 4π | B. | 2π | C. | π | D. | $\frac{π}{2}$ |
10.已知圆C:x2+y2=4,直线l:y=x,则圆C上任取一点A到直线l的距离小于1的概率为( )
| A. | $\frac{3}{4}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{3}$ |
9.若$\frac{1+ai}{2+i}=1+2i$,则a=( )
| A. | -5-i | B. | -5+i | C. | 5-i | D. | 5+i |
8.已知集合A={x|0<x<2},B={x|x2-1<0},则A∪B=( )
| A. | (-1,1) | B. | (-1,2) | C. | (1,2) | D. | (0,1) |
7.若复数z=1+i,$\overline z$为z的共轭复数,则z•$\overline z$=( )
0 239364 239372 239378 239382 239388 239390 239394 239400 239402 239408 239414 239418 239420 239424 239430 239432 239438 239442 239444 239448 239450 239454 239456 239458 239459 239460 239462 239463 239464 239466 239468 239472 239474 239478 239480 239484 239490 239492 239498 239502 239504 239508 239514 239520 239522 239528 239532 239534 239540 239544 239550 239558 266669
| A. | 0 | B. | 2 | C. | $\sqrt{2}$ | D. | 2i |