题目内容
12．若二项式${（{{x^2}-\frac{2}{x}}）^n}$展开式的二项式系数之和为8，则该展开式的系数之和为（ ）| A． | -1 | B． | 1 | C． | 27 | D． | -27 |
分析 根据二项式展开式的二项式系数之和2n，求出n的值；再令x=1求出二项式展开式的系数之和．
解答 解：二项式${（{{x^2}-\frac{2}{x}}）^n}$展开式的二项式系数之和为8，
所以2n=8，解得n=3；
所以${{（x}^{2}-\frac{2}{x}）}^{3}$展开式的系数之和为：
（1-2）3=-1．
故选：A．
点评 本题考查了二项式展开式的二项式系数之和与展开式的各项系数之和的计算问题，是基础题．
练习册系列答案
相关题目
2．满足A=60°，a=2$\sqrt{3}$，b=4的△ABC的个数是（ ）
| A． | 0 | B． | 1 | C． | 2 | D． | 3 |
3．
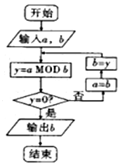如图的程序框图的算法思路源于数学名著《几何原本》中的“辗转相除法”，执行该程序框图（图中“aMODb”表示a除以b的余数），若输入的a，b分别为485，270，则输出的b=（ ）
如图的程序框图的算法思路源于数学名著《几何原本》中的“辗转相除法”，执行该程序框图（图中“aMODb”表示a除以b的余数），若输入的a，b分别为485，270，则输出的b=（ ）| A． | 0 | B． | 10 | C． | 5 | D． | 55 |
7．若复数z=1+i，$\overline z$为z的共轭复数，则z•$\overline z$=（ ）
| A． | 0 | B． | 2 | C． | $\sqrt{2}$ | D． | 2i |
4．已知函数$f（x）=sin\frac{πx}{6}$，集合M={0，1，2，3，4，5，6，7，8}，现从M中任取两个不同元素m，n，则f（m）f（n）=0的概率为（ ）
| A． | $\frac{5}{12}$ | B． | $\frac{7}{12}$ | C． | $\frac{7}{18}$ | D． | $\frac{7}{9}$ |