题目内容
10.已知圆C:x2+y2=4,直线l:y=x,则圆C上任取一点A到直线l的距离小于1的概率为( )| A. | $\frac{3}{4}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{3}$ |
分析 设和直线l平行的直线的方程为x-y+c=0根据点到直线的距离公式和解三角形的有关知识可得符合条件的圆心角的度数为4×30°=120°,根据概率公式计算即可
解答  解:设和直线l平行的直线的方程为x-y+c=0,
解:设和直线l平行的直线的方程为x-y+c=0,
∵圆C上任取一点A到直线l的距离小于1,
∴圆心到直线x-y+c=0的距离小于1,
∴$\frac{|c|}{\sqrt{2}}$≤1,
解得|c|≤$\sqrt{2}$,
分别做直线y=x+$\sqrt{2}$和y=x-$\sqrt{2}$,如图所示,
∵OC=1,OB=2,
∴∠CBO=30°,
∴∠AOB=30°,
∴符合条件的圆心角的度数为4×30°=120°,
根据几何概型的概率公式得到P=$\frac{120}{360}$=$\frac{1}{3}$,
故选:D
点评 本题考查概率的求法,解题时要认真审题,注意圆的性质及点到直线的距离公式的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20.已知函数f(x)=cos($\frac{2π}{3}$x)+(a-1)sin($\frac{π}{3}$x)+a,g(x)=3x-x,若f(g(x))≤0对任意的x∈[0,1]恒成立,则实数a的取值范围是( )
| A. | (-∞,$\sqrt{3}$-1] | B. | (-∞,0] | C. | [0,$\sqrt{3}$-1] | D. | (-∞,1-$\sqrt{3}$] |
15.在△ABC中,A=60°,b=1,${S_{△ABC}}=\sqrt{3}$,则$\frac{c}{sinC}$=( )
| A. | $\frac{{8\sqrt{3}}}{81}$ | B. | $\frac{{2\sqrt{39}}}{3}$ | C. | $\frac{{26\sqrt{3}}}{3}$ | D. | $2\sqrt{7}$ |
 如图,O为坐标原点,点F为抛物线C1:x2=2py(p>0)的焦点,且抛物线C1上点M处的切线与圆C2:x2+y2=1相切于点Q.
如图,O为坐标原点,点F为抛物线C1:x2=2py(p>0)的焦点,且抛物线C1上点M处的切线与圆C2:x2+y2=1相切于点Q.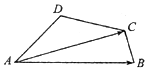 在四边形ABCD中,∠ADC=∠BCD=120°,AD=DC=2CB=1,则$\overrightarrow{AB}$•$\overrightarrow{AC}$=3.
在四边形ABCD中,∠ADC=∠BCD=120°,AD=DC=2CB=1,则$\overrightarrow{AB}$•$\overrightarrow{AC}$=3.