题目内容
11.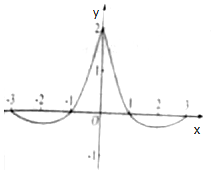 已知函数f(x)=$\frac{{cos({ωx+φ})}}{{a•{e^{|x|}}}}$(ω>0,|φ|<$\frac{π}{2}$,a∈R)在区间[-3,3]上的图象如图所示,则$\frac{ω}{a}$可取( )
已知函数f(x)=$\frac{{cos({ωx+φ})}}{{a•{e^{|x|}}}}$(ω>0,|φ|<$\frac{π}{2}$,a∈R)在区间[-3,3]上的图象如图所示,则$\frac{ω}{a}$可取( )| A. | 4π | B. | 2π | C. | π | D. | $\frac{π}{2}$ |
分析 根据f(x)的奇偶性,特殊值计算a,ω,φ的值即可得出答案.
解答 解:由图象可知f(x)是偶函数,∴φ=kπ,又|φ|<$\frac{π}{2}$,∴φ=0.
令f(x)=0得cosωx=0,∴ωx=$\frac{π}{2}$+kπ,解得x=$\frac{π}{2ω}$+$\frac{kπ}{ω}$,k∈Z.
∵ω>0,∴f(x)的最小正零点为$\frac{π}{2ω}$,
由图象可知f(x)的最小正零点为1,故$\frac{π}{2ω}$=1,解得ω=$\frac{π}{2}$,
∴f(x)=$\frac{cos\frac{π}{2}x}{a•{e}^{|x|}}$,
由图象f(0)=2,故$\frac{1}{a}$=2,∴a=$\frac{1}{2}$,
∴$\frac{ω}{a}$=π.
故选C.
点评 本题考查了三角函数的图象与性质,属于中档题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
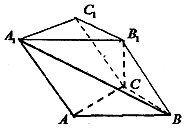 如图,斜三棱柱ABC-A1B1C1中,侧面AA1B1B为菱形,底面△ABC是等腰直角三角形,∠BAC=90°,A1B⊥B1C.
如图,斜三棱柱ABC-A1B1C1中,侧面AA1B1B为菱形,底面△ABC是等腰直角三角形,∠BAC=90°,A1B⊥B1C.