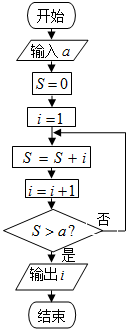
8．按如图所示的程序框图.若输入a=81.则输出的i=( )A．14B．17C．19D．21——青夏教育精英家教网——

8．按如图所示的程序框图，若输入a=81，则输出的i=（　　）

7．阅读程序框图，该算法的功能是输出（　　）

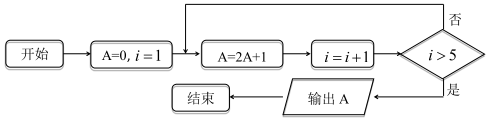
	A．	数列{2^n-1}的前 4项的和		B．	数列{2ⁿ-1}的第4项
	C．	数列{2ⁿ}的前5项的和		D．	数列?{2ⁿ-1}的第5项

6．已知椭圆$C：\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（{a＞b＞c}）$的长轴长为 4，离心率为$\frac{{\sqrt{6}}}{3}$．
（1）求椭圆 C的方程；
（2）过椭圆 C上的任意一点 P，向圆O：x²+y²=r²（0＜r＜b）引两条切线l₁，l₂，若l₁，l₂的斜率乘积恒为定值，求圆 O的面积．

5．已知数列{a_n}的前 n项和为 S_n，且满足a₁=1，a_n•a_n+1=2S_n，设${b_n}=\frac{{2{a_n}-1}}{{{3^{a_n}}}}$，则数列{b_n}的前 n项和为$1-\frac{n+1}{3^n}$．

4．在平面直角坐标系 xOy中，已知抛物线E：y²=2px（p＞0）的焦点为F，P是抛物线 E上位于第一象限内的任意一点，Q是线段 PF上的点，且满足$\overrightarrow{OQ}=\frac{2}{3}\overrightarrow{OP}+\frac{1}{3}\overrightarrow{OF}$，则直线 OQ的斜率的最大值为（　　）

$\frac{{\sqrt{2}}}{2}$

3．执行如图所示的程序框图，则输出 S的值为（　　）

2．已知椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$（a＞b＞0）的离心率为$\frac{{\sqrt{3}}}{2}$，且过点M（4，1）．
（Ⅰ）求椭圆C的方程；
（Ⅱ）若直线l：y=x+m（m≠-3）与椭圆C交于P，Q两点，记直线MP，MQ的斜率分别为k₁，k₂，试探究k₁+k₂是否为定值．若是，请求出该定值；若不是，请说明理由．

1．已知点P₁（x₁，y₁），P₂（x₂，y₂），P₃（x₃，y₃），P₄（x₄，y₄），P₅（x₅，y₅），P₆（x₆，y₆）是抛物线C：y²=2px（p＞0）上的点，F是抛物线C的焦点，若|P₁F|+|P₂F|+|P₃F|+|P₄F|+|P₅F|+|P₆F|=36，且x₁+x₂+x₃+x₄+x₅+x₆=24，则抛物线C的方程为（　　）

20．已知命题p：?x∈（1，+∞），x³+16＞8x，则命题p的否定为（　　）

	A．	?x∈（1，+∞），x³+16≤8x		B．	?x∈（1，+∞），x³+16＜8x
	C．	?x∈（1，+∞），x³+16≤8x		D．	?x∈（1，+∞），x³+16＜8x

19．$\frac{{{i^{2017}}}}{1-2i}$=（　　）

$-\frac{2}{5}+\frac{1}{5}i$

$\frac{2}{5}-\frac{1}{5}i$

$\frac{2}{5}+\frac{1}{5}i$

$-\frac{2}{5}-\frac{1}{5}i$

0 239259 239267 239273 239277 239283 239285 239289 239295 239297 239303 239309 239313 239315 239319 239325 239327 239333 239337 239339 239343 239345 239349 239351 239353 239354 239355 239357 239358 239359 239361 239363 239367 239369 239373 239375 239379 239385 239387 239393 239397 239399 239403 239409 239415 239417 239423 239427 239429 239435 239439 239445 239453 266669