题目内容
2.已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的离心率为$\frac{{\sqrt{3}}}{2}$,且过点M(4,1).(Ⅰ)求椭圆C的方程;
(Ⅱ)若直线l:y=x+m(m≠-3)与椭圆C交于P,Q两点,记直线MP,MQ的斜率分别为k1,k2,试探究k1+k2是否为定值.若是,请求出该定值;若不是,请说明理由.
分析 (Ⅰ)由椭圆的离心率公式,求得a2=4b2,将M代入椭圆方程,即可求得a和b的值,求得椭圆方程;
(Ⅱ)将直线l:代入椭圆方程,利用韦达定理及直线的斜率公式,即可取得k1+k2=0.
解答 解:(Ⅰ)依题意,e=$\frac{c}{a}$=$\sqrt{1-\frac{{b}^{2}}{{a}^{2}}}$=$\frac{{\sqrt{3}}}{2}$,则a2=4b2,
由椭圆过点M(4,1),代入椭圆方程:$\frac{{x}^{2}}{4{b}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$,解得:b2=5,a2=20,
∴椭圆的标准方程:$\frac{{x}^{2}}{20}+\frac{{y}^{2}}{5}=1$;
(Ⅱ)k1+k2为定值0,下面给出证明,
设P(x1,y1),P(x2,y2),
则$\left\{\begin{array}{l}{y=x+m}\\{\frac{{x}^{2}}{20}+\frac{{y}^{2}}{5}=1}\end{array}\right.$,整理得:5x2+8mx+2m2-20=0,
△=(8m)2-4×5×(2m2-20)>0,解得:-5<m<5,且m≠-3,
则x1+x2=-$\frac{8m}{5}$,x1x2=$\frac{4{m}^{2}-20}{5}$,
则k1+k2=$\frac{{y}_{1}-1}{{x}_{1}-4}$+$\frac{{y}_{2}-1}{{x}_{2}-4}$=$\frac{({y}_{1}-1)({x}_{2}-4)+({y}_{2}-1)({x}_{1}-4)}{({x}_{1}-4)({x}_{2}-4)}$,
则(y1-1)(x2-4)+(y2-1)(x1-4)=(x1+m-1)(x2-4)+(x2+m-1)(x1-4),
=2x1x2+(m-5)(x1+x2)-8(m-1),
=2×$\frac{4{m}^{2}-20}{5}$+(m-5)(-$\frac{8m}{5}$)-8(m-1),
=0,
∴k1+k2=0,
∴k1+k2为定值0.
点评 本题考查椭圆的标准方程,直线与椭圆的位置关系,考查韦达定理,直线的斜率公式,考查计算能力,属于中档题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案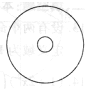 如图,半径为5cm的圆形纸板内有一个相同圆心的半径为1cm的小圆,现将半径为1cm的一枚硬币抛到此纸板上,使整块硬币完全随机落在纸板内,则硬币与小圆无公共点的概率为( )
如图,半径为5cm的圆形纸板内有一个相同圆心的半径为1cm的小圆,现将半径为1cm的一枚硬币抛到此纸板上,使整块硬币完全随机落在纸板内,则硬币与小圆无公共点的概率为( )| A. | $\frac{1}{2}$ | B. | $\frac{21}{25}$ | C. | $\frac{1}{4}$ | D. | $\frac{3}{4}$ |
| A. | -1 | B. | -i | C. | $\sqrt{2}i$ | D. | $-\sqrt{2}$ |
| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{2\sqrt{3}}{3}$ | C. | $\sqrt{3}$ | D. | $\frac{4\sqrt{3}}{3}$ |
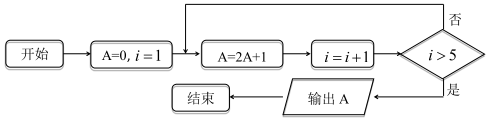
| A. | 数列{2n-1}的前 4项的和 | B. | 数列{2n-1}的第4项 | ||
| C. | 数列{2n}的前5项的和 | D. | 数列?{2n-1}的第5项 |
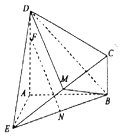 如图所示的几何体ABCDE中,DA⊥平面EAB,CB∥DA,EA=DA=AB=2CB,EA⊥
如图所示的几何体ABCDE中,DA⊥平面EAB,CB∥DA,EA=DA=AB=2CB,EA⊥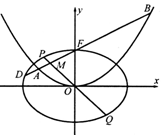 如图,在平面直角坐标系xOy中,椭圆C1:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的离心率为$\frac{{\sqrt{3}}}{2}$,抛物线C2:x2=4y的焦点F是C1的一个顶点.
如图,在平面直角坐标系xOy中,椭圆C1:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的离心率为$\frac{{\sqrt{3}}}{2}$,抛物线C2:x2=4y的焦点F是C1的一个顶点.