16.设点M(x,y)满足不等式组$\left\{\begin{array}{l}3x-y-6≤0\\ x-y+2≥0\\ x≥0,y≥0\end{array}\right.$,点P(-4a,a)(a>0),则当$\overrightarrow{OP}•\overrightarrow{OM}$最大时,点M为( )
| A. | (0,2) | B. | (0,0) | C. | (4,6) | D. | (2,6) |
15.现有4人参加抽奖活动,每人依次从装有4张奖票(其中2张为中奖票)的箱子中不放回地随机抽取一张,直到2张中奖票都被抽出时活动结束,则活动恰好在第3人抽完后结束的概率为( )
| A. | $\frac{1}{10}$ | B. | $\frac{1}{5}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
14.已知x>0,y>0,$\frac{2}{x}+\frac{1}{y}=\frac{1}{3}$,x+2y>m2-2m恒成立,则m的取值范围是( )
| A. | [-6,4] | B. | [-4,6] | C. | (-4,6) | D. | (-6,4) |
13.已知复数z=|1-i|i2017(其中i为虚数单位),则$\overline z$的虚部为( )
| A. | -1 | B. | -i | C. | $\sqrt{2}i$ | D. | $-\sqrt{2}$ |
12.已知全集U=R,集合A={x|x2-2x-8>0},B={1,5},则集合(∁UA)∩B为( )
| A. | {x|1<x<5} | B. | {x|x>5} | C. | {1} | D. | {1,5} |
9.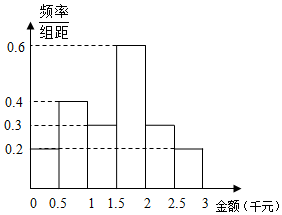 某网络营销部门为了统计某市网友2016年12月12日的网购情况,从该市当天参与网购的顾客中随机抽查了男女各30人,统计其网购金额,得到如下频率分布直方图:
某网络营销部门为了统计某市网友2016年12月12日的网购情况,从该市当天参与网购的顾客中随机抽查了男女各30人,统计其网购金额,得到如下频率分布直方图:
若网购金额超过2千元的顾客称为“网购达人”,网购金额不超过2千元的顾客称为“非网购达人”.
( I)根据频率分布直方图估计网友购物金额的平均值;
( II)若抽取的“网购达人”中女性占12人,请根据条件完成上面的2×2列联表,并判断是否有99%的把握认为“网购达人”与性别有关?
(参考公式:${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d)
0 239256 239264 239270 239274 239280 239282 239286 239292 239294 239300 239306 239310 239312 239316 239322 239324 239330 239334 239336 239340 239342 239346 239348 239350 239351 239352 239354 239355 239356 239358 239360 239364 239366 239370 239372 239376 239382 239384 239390 239394 239396 239400 239406 239412 239414 239420 239424 239426 239432 239436 239442 239450 266669
 某网络营销部门为了统计某市网友2016年12月12日的网购情况,从该市当天参与网购的顾客中随机抽查了男女各30人,统计其网购金额,得到如下频率分布直方图:
某网络营销部门为了统计某市网友2016年12月12日的网购情况,从该市当天参与网购的顾客中随机抽查了男女各30人,统计其网购金额,得到如下频率分布直方图:| 网购达人 | 非网购达人 | 合计 | |
| 男性 | 30 | ||
| 女性 | 12 | 30 | |
| 合计 | 60 |
( I)根据频率分布直方图估计网友购物金额的平均值;
( II)若抽取的“网购达人”中女性占12人,请根据条件完成上面的2×2列联表,并判断是否有99%的把握认为“网购达人”与性别有关?
(参考公式:${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d)
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
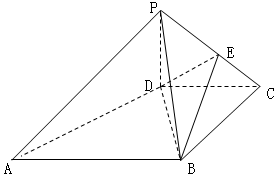 如图,在四棱锥P-ABCD中,底面ABCD是梯形,AB∥CD,PD⊥平面ABCD,BD⊥DC,PD=BD=DC=$\frac{1}{2}$AB,E为PC中点.
如图,在四棱锥P-ABCD中,底面ABCD是梯形,AB∥CD,PD⊥平面ABCD,BD⊥DC,PD=BD=DC=$\frac{1}{2}$AB,E为PC中点.