已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$一条渐近线与x轴的夹角为30°.那么双曲线的离心率为$\frac{2\sqrt{3}}{3}$．题目和参考答案——青夏教育精英家教网——

题目内容

18．已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（{a＞0，b＞0}）$一条渐近线与x轴的夹角为30°，那么双曲线的离心率为$\frac{2\sqrt{3}}{3}$．

分析由双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（{a＞0，b＞0}）$一的一条渐近线与x轴的夹角为30°，可得 $\frac{b}{a}$=tan30°=$\frac{\sqrt{3}}{3}$，利用e=$\frac{c}{a}$=转化求出双曲线的离心率．

解答解：∵双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（{a＞0，b＞0}）$一条渐近线与x轴的夹角为30°，
∴$\frac{b}{a}$=tan30°=$\frac{\sqrt{3}}{3}$，
∴e=$\frac{c}{a}$=$\sqrt{1+（\frac{b}{a}）^{2}}$=$\frac{2\sqrt{3}}{3}$．
故答案为：$\frac{{2\sqrt{3}}}{3}$．

点评本题考查了双曲线的几何性质，由渐近线的斜率推导双曲线的离心率是解决本题的关键．

练习册系列答案

名校课堂系列答案

西城学科专项测试系列答案

小考必做系列答案

小考实战系列答案

小考复习精要系列答案

小考总动员系列答案

小升初必备冲刺48天系列答案

68所名校图书小升初高分夺冠真卷系列答案

伴你成长周周练月月测系列答案

小升初金卷导练系列答案

相关题目

8．已知函数f（x）=cos（2x-$\frac{π}{6}$）+sin2x，则f（x）的一个单调递减区间是（　　）

[-$\frac{π}{3}$，$\frac{π}{6}$]

[-$\frac{π}{3}$，$\frac{2π}{3}$]

[-$\frac{π}{6}$，$\frac{5π}{6}$]

[$\frac{π}{6}$，$\frac{2π}{3}$]

9．执行所给的程序框图，则输出的值是（　　）

6．已知向量$\overrightarrow{a}$=（k，k+1），$\overrightarrow{b}$=（1，-2）且$\overrightarrow{a}$∥$\overrightarrow{b}$，则实数k等于$-\frac{1}{3}$．

13．已知复数z=|1-i|i²⁰¹⁷（其中i为虚数单位），则$\overline z$的虚部为（　　）

3．等腰直角三角形ABC中，∠C=90°，AC=BC=2，点P是△ABC斜边上任意一点，则线段CP的长度不大于$\sqrt{3}$的概率是（　　）

$\frac{{\sqrt{2}}}{2}$

$\frac{{\sqrt{2}}}{4}$

$\frac{{\sqrt{6}}}{4}$

10．已知三棱锥P-ABC的各顶点都在同一球的面上，且PA⊥平面ABC，若球O的体积为$\frac{20\sqrt{5}π}{3}$（球的体积公式为$\frac{4π}{3}$R³，其中R为球的半径），AB=2，AC=1，∠BAC=60°，则三棱锥P-ABC的体积为（　　）

$\frac{\sqrt{3}}{3}$

$\frac{2\sqrt{3}}{3}$

$\frac{4\sqrt{3}}{3}$

7．阅读程序框图，该算法的功能是输出（　　）

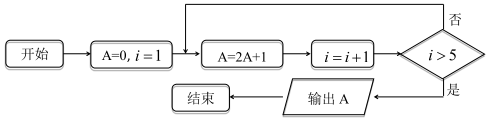
	A．	数列{2^n-1}的前 4项的和		B．	数列{2ⁿ-1}的第4项
	C．	数列{2ⁿ}的前5项的和		D．	数列?{2ⁿ-1}的第5项

8．在平面直角坐标系xOy中，已知抛物线C：x²=4y，点P是C的准线l上的动点，过点P作C的两条切线，切点分别为A，B，则△AOB面积的最小值为（　　）