题目内容

13．已知复数z=|1-i|i2017（其中i为虚数单位），则$\overline z$的虚部为（　　）
A．-1B．-iC．$\sqrt{2}i$D．$-\sqrt{2}$

分析 利用复数的周期性、模的计算公式、虚部的定义即可得出．

解答 解：∵i4=1，∴i2017=（i4）504•i=i．
∴z=|1-i|i2017=$\sqrt{2}$i．
∴$\overline{z}$=-$\sqrt{2}$i的虚部为-$\sqrt{2}$．
故选：D．

点评 本题考查了复数的周期性、模的计算公式、虚部的定义，考查了推理能力与计算能力，属于基础题．

练习册系列答案
相关题目
3．设T?R，若存在常数M＞0，使得对任意t∈T，均有|t|≤M，则称T为有界集合，同时称M为集合T的上界．
（1）设A1={y|y=$\frac{{2}^{x}-1}{{2}^{x}+1}$，x∈R}，A2={x|sinx＞$\frac{1}{2}$}，试判断A1、A2是否为有界集合，并说明理由；
（2）已知f（x）=x2+u，记f1（x）=f（x），fn（x）=f（fn-1（x））（n=2，3，…），若m∈R，u∈[$\frac{1}{4}$，+∞），且B={fn（m）|n∈N*}为有界集合，求u的值及m的取值范围；
（3）设a，b，c均为正数，将（a-b）2、（b-c）2、（c-a）2中的最小值记为d，是否存在正数λ∈（0，1），使得λ为有界集合C={y|$\frac{d}{{a}^{2}+{b}^{2}+{c}^{2}}$，a、b、c均为正数}的上界，若存在，试求λ的最小值；若不存在，请说明理由．
4．在锐角△ABC中，内角A，B，C的对边分别为a，b，c，且（c+b）（sinC-sinB）=a（sinA-sinB）．若c=2$\sqrt{3}$，则a2+b2的取值范围是（20，24]．
1．已知函数f（x）=xlnx-mx的图象与直线y=-1相切．
（Ⅰ）求m的值，并求f（x）的单调区间；
（Ⅱ）若g（x）=ax3，设h（x）=f（x）-g（x），讨论函数h（x）的零点个数．
8．已知数列{an}满足a1=-2，an+1=2an+4．
（ I）求证{an+4}是等比数列，并求数列{an}的通项公式；
（ II）求数列{an}的前n项的和Sn．
18．已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（{a＞0，b＞0}）$一条渐近线与x轴的夹角为30°，那么双曲线的离心率为$\frac{2\sqrt{3}}{3}$．
5．若执行如图的程序框图，输出S的值为-2，则判断框中应填入的条件是（　　）
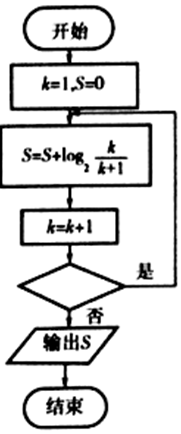
A．k＜2B．k＜3C．k＜4D．k＜5
2．已知椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$（a＞b＞0）的离心率为$\frac{{\sqrt{3}}}{2}$，且过点M（4，1）．
（Ⅰ）求椭圆C的方程；
（Ⅱ）若直线l：y=x+m（m≠-3）与椭圆C交于P，Q两点，记直线MP，MQ的斜率分别为k1，k2，试探究k1+k2是否为定值．若是，请求出该定值；若不是，请说明理由．
3．已知函数f（x）=xex．
（Ⅰ）讨论函数g（x）=af（x）+ex的单调性；
（Ⅱ）若直线y=x+2与曲线y=f（x）的交点的横坐标为t，且t∈[m，m+1]，求整数m所有可能的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网