题目内容
17.已知f(x)=(x-4)3+x-1,{an}是公差不为0的等差数列,f(a1)+f(a2)+…+f(a9)=27,则f(a5)的值为( )| A. | 0 | B. | 1 | C. | 3 | D. | 5 |
分析 f(x)=(x-4)3+x-1,可得f(x)-3=(x-4)3+x-4,令x-4=t,可得函数g(t)=t3+t为奇函数且单调递增.{an}是公差不为0的等差数列,可得a1+a9=a2+a8=a3+a7=a4+a6=2a5.由f(a1)+f(a2)+…+f(a9)
=27,可得g(a1)+g(a2)+…+g(a9)=0,因此g(a5)=0,即可得出.
解答 解:∵f(x)=(x-4)3+x-1,
∴f(x)-3=(x-4)3+x-4=g(x-4),
令x-4=t,可得函数g(t)=t3+t为奇函数且单调递增.
{an}是公差不为0的等差数列,∴a1+a9=a2+a8=a3+a7=a4+a6=2a5.
∵f(a1)+f(a2)+…+f(a9)=27,
∴g(a1)+g(a2)+…+g(a9)=0,
∴g(a5)=0,
则f(a5)=g(a5)+3=3.
故选:C.
点评 本题考查了等差数列通项公式及其性质、函数的奇偶性与单调性、构造函数方法,考查了推理能力与计算能力,属于难题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.设函数f(x)=|x2-2x-1|,若m>n>1,且f(m)=f(n),则(m-1)(n-1)的取值范围为( )
| A. | (0,2) | B. | (0,2] | C. | (1,2) | D. | (1,2] |
12.已知全集U=R,集合A={x|x2-2x-8>0},B={1,5},则集合(∁UA)∩B为( )
| A. | {x|1<x<5} | B. | {x|x>5} | C. | {1} | D. | {1,5} |
2.下列命题正确的是( )
| A. | “x<-2”是“x2+3x+2>0”的必要不充分条件 | |
| B. | 对于命题p:?x0∈R,使得${x_0}^2+{x_0}-1<0$,则¬p:?x∈R,均有x2+x-1≥0 | |
| C. | 命题“若x2-3x+2=0,则x=2”的否命题为若x2-3x+2=0,则x≠2 | |
| D. | 若p∧q为假命题,则p,q均为假命题 |
9.已知双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的一条渐近线方程为x-ay=0,曲线C的一个焦点与抛物线y2=-8x的焦点重合,则双曲线的离心率为( )
| A. | $\frac{2\sqrt{3}}{3}$ | B. | $\sqrt{2}$ | C. | 2 | D. | $\sqrt{10}$ |
7.执行如图所示的程序框图,如图输出S的值为-1,那么判断框内应填入的条件是( )
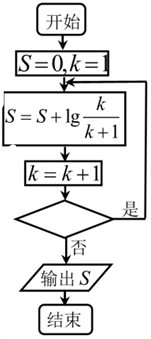

| A. | k≤8 | B. | k≤9 | C. | k≤10 | D. | k≤11 |