题目内容
14.已知x>0,y>0,$\frac{2}{x}+\frac{1}{y}=\frac{1}{3}$,x+2y>m2-2m恒成立,则m的取值范围是( )| A. | [-6,4] | B. | [-4,6] | C. | (-4,6) | D. | (-6,4) |
分析 利用基本不等式求出xy的范围,从而得出x+2y的范围,根据不等式恒成立得出关于m的一元二次不等式,从而解出m的范围.
解答 解:∵$\frac{2}{x}+\frac{1}{y}$≥2$\sqrt{\frac{2}{xy}}$,即$\frac{1}{3}$≥2$\sqrt{\frac{2}{xy}}$,解得xy≥72,
∵$\frac{2}{x}+\frac{1}{y}=\frac{1}{3}$,∴$\frac{6}{x}+\frac{3}{y}=1$,即3x+6y=xy,
∴x+2y=$\frac{1}{3}$xy≥24,
∴m2-2m<24恒成立,
解不等式m2-2m-24<0得-4<m<6.
故选:C.
点评 本题考查了不等式的性质,一元二次不等式的解法,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.已知向量$\overrightarrow{a}$,$\overrightarrow{b}$为单位向量,且|$\overrightarrow{b}$|=|$\overrightarrow{a}$|=|$\overrightarrow{a}$-$\overrightarrow{b}$|=1,则|2$\overrightarrow{a}$+$\overrightarrow{b}$|=( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\sqrt{5}$ | D. | $\sqrt{7}$ |
2.已知双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的渐近线方程为y=±$\frac{3}{4}$x,则双曲线C的离心率为( )
| A. | $\frac{{\sqrt{7}}}{2}$ | B. | $\frac{5}{3}$ | C. | $\frac{{\sqrt{7}}}{3}$ | D. | $\frac{5}{4}$ |
9.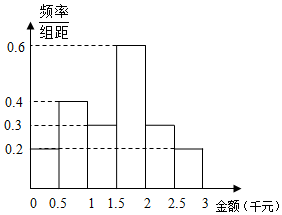 某网络营销部门为了统计某市网友2016年12月12日的网购情况,从该市当天参与网购的顾客中随机抽查了男女各30人,统计其网购金额,得到如下频率分布直方图:
某网络营销部门为了统计某市网友2016年12月12日的网购情况,从该市当天参与网购的顾客中随机抽查了男女各30人,统计其网购金额,得到如下频率分布直方图:
若网购金额超过2千元的顾客称为“网购达人”,网购金额不超过2千元的顾客称为“非网购达人”.
( I)根据频率分布直方图估计网友购物金额的平均值;
( II)若抽取的“网购达人”中女性占12人,请根据条件完成上面的2×2列联表,并判断是否有99%的把握认为“网购达人”与性别有关?
(参考公式:${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d)
 某网络营销部门为了统计某市网友2016年12月12日的网购情况,从该市当天参与网购的顾客中随机抽查了男女各30人,统计其网购金额,得到如下频率分布直方图:
某网络营销部门为了统计某市网友2016年12月12日的网购情况,从该市当天参与网购的顾客中随机抽查了男女各30人,统计其网购金额,得到如下频率分布直方图:| 网购达人 | 非网购达人 | 合计 | |
| 男性 | 30 | ||
| 女性 | 12 | 30 | |
| 合计 | 60 |
( I)根据频率分布直方图估计网友购物金额的平均值;
( II)若抽取的“网购达人”中女性占12人,请根据条件完成上面的2×2列联表,并判断是否有99%的把握认为“网购达人”与性别有关?
(参考公式:${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d)
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
6.执行如图所示的程序框图,若输入t的值为5,则输出的S的值为( )
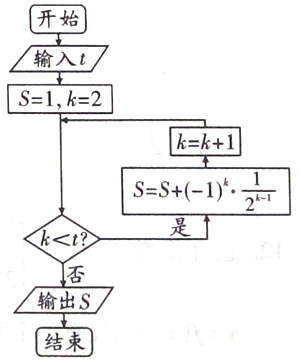

| A. | $\frac{11}{8}$ | B. | $\frac{9}{16}$ | C. | $\frac{5}{4}$ | D. | $\frac{21}{16}$ |
3.执行如图所示的程序框图,则输出 S的值为( )


| A. | -lg9 | B. | -1 | C. | -lg11 | D. | 1 |