题目内容
15.现有4人参加抽奖活动,每人依次从装有4张奖票(其中2张为中奖票)的箱子中不放回地随机抽取一张,直到2张中奖票都被抽出时活动结束,则活动恰好在第3人抽完后结束的概率为( )| A. | $\frac{1}{10}$ | B. | $\frac{1}{5}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
分析 活动恰好在第3人抽完后结束,由指前两人中一人抽到中奖票,另一人抽到没有中奖的票,第三人抽到中奖票,由此能求出活动恰好在第3人抽完后结束的概率.
解答 解:∵活动恰好在第3人抽完后结束,
∴前两人中一人抽到中奖票,另一人抽到没有中奖的票,
第三人抽到中奖票,
∴活动恰好在第3人抽完后结束的概率:
P=($\frac{2}{4}×\frac{2}{3}$+$\frac{2}{4}×\frac{2}{3}$)×$\frac{1}{2}$=$\frac{1}{3}$.
故选:C.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意相互独立事件概率乘法公式和互斥事件概率加法公式的合理运用.

练习册系列答案
相关题目
5.已知tanx=-$\frac{1}{2}$,则2sinxcosx=( )
| A. | -$\frac{4}{5}$ | B. | -3 | C. | -$\frac{7}{5}$ | D. | -$\frac{11}{5}$ |
6.2017年3月27日,一则“清华大学要求从2017级学生开始,游泳达到一定标准才能毕业”的消息在体育界和教育界引起了巨大反响.游泳作为一项重要的求生技能和运动项目受到很多人的喜爱.其实,已有不少高校将游泳列为必修内容.某中学为了解2017届高三学生的性别和喜爱游泳是否有关,对100名高三学生进行了问卷调查,得到如下列联表:
已知在这100人中随机抽取1人,抽到喜欢游泳的学生的概率为$\frac{3}{5}$.
(Ⅰ)请将上述列联表补充完整;
(Ⅱ)判断是否有99.9%的把握认为喜欢游泳与性别有关?
附:${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$
| 喜欢游泳 | 不喜欢游泳 | 合计 | |
| 男生 | 10 | ||
| 女生 | 20 | ||
| 合计 |
(Ⅰ)请将上述列联表补充完整;
(Ⅱ)判断是否有99.9%的把握认为喜欢游泳与性别有关?
附:${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$
| p(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
3.把函数f(x)=$\sqrt{3}$cos2x-sin2x的图象向右平移$\frac{π}{12}$个单位得到函数y=g(x)的图象,则函数y=g(x)在下列哪个区间是单调递减的( )
| A. | [-$\frac{π}{2}$,0] | B. | [-π,0] | C. | [-$\frac{π}{4}$,$\frac{π}{4}$] | D. | [0,$\frac{π}{2}$] |
20.为了解人们对城市治安状况的满意度,某部门对城市部分居民的“安全感”进行调查,在调查过程中让每个居民客观地对自己目前生活城市的安全感进行评分,并把所得分作为“安全感指数”,即用区间[0,100]内的一个数来表示,该数越接近100表示安全感越高.现随机对该地区的男、女居民各500人进行了调查,调查数据如表所示:
根据表格,解答下面的问题:
(Ⅰ)估算该地区居民安全感指数的平均值;
(Ⅱ)如果居民安全感指数不小于60,则认为其安全感好.为了进一步了解居民的安全感,调查组又在该地区随机抽取3对夫妻进行调查,用X表示他们之中安全感好的夫妻(夫妻二人都感到安全)的对数,求X的分布列及期望(以样本的频率作为总体的概率).
| 安全感指数 | [0,20) | [20,40) | [40,60) | [60,80) | [80,100] |
| 男居民人数 | 8 | 16 | 226 | 131 | 119 |
| 女居民人数 | 12 | 14 | 174 | 122 | 178 |
(Ⅰ)估算该地区居民安全感指数的平均值;
(Ⅱ)如果居民安全感指数不小于60,则认为其安全感好.为了进一步了解居民的安全感,调查组又在该地区随机抽取3对夫妻进行调查,用X表示他们之中安全感好的夫妻(夫妻二人都感到安全)的对数,求X的分布列及期望(以样本的频率作为总体的概率).
7.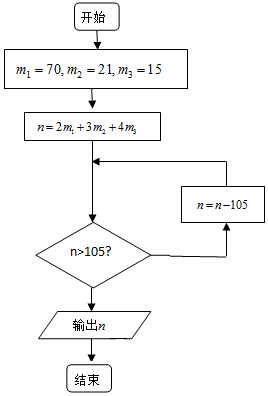 明朝数学家程大位将“孙子定理”(也称“中国剩余定理”)编成易于上口的《孙子口诀》:三人同行七十稀,五树梅花廿一支,七子团圆正半月,除百零五便得知.已知正整数n被3除余2,被5除余3,被7除余4,求n的最小值.按此口诀的算法如图,则输出n的结果为( )
明朝数学家程大位将“孙子定理”(也称“中国剩余定理”)编成易于上口的《孙子口诀》:三人同行七十稀,五树梅花廿一支,七子团圆正半月,除百零五便得知.已知正整数n被3除余2,被5除余3,被7除余4,求n的最小值.按此口诀的算法如图,则输出n的结果为( )
 明朝数学家程大位将“孙子定理”(也称“中国剩余定理”)编成易于上口的《孙子口诀》:三人同行七十稀,五树梅花廿一支,七子团圆正半月,除百零五便得知.已知正整数n被3除余2,被5除余3,被7除余4,求n的最小值.按此口诀的算法如图,则输出n的结果为( )
明朝数学家程大位将“孙子定理”(也称“中国剩余定理”)编成易于上口的《孙子口诀》:三人同行七十稀,五树梅花廿一支,七子团圆正半月,除百零五便得知.已知正整数n被3除余2,被5除余3,被7除余4,求n的最小值.按此口诀的算法如图,则输出n的结果为( )| A. | 53 | B. | 54 | C. | 158 | D. | 263 |
4.在平面直角坐标系 xOy中,已知抛物线E:y2=2px(p>0)的焦点为F,P是抛物线 E上位于第一象限内的任意一点,Q是线段 PF上的点,且满足$\overrightarrow{OQ}=\frac{2}{3}\overrightarrow{OP}+\frac{1}{3}\overrightarrow{OF}$,则直线 OQ的斜率的最大值为( )
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\sqrt{3}$ | C. | 1 | D. | $\sqrt{2}$ |
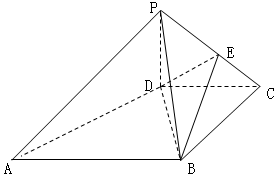 如图,在四棱锥P-ABCD中,底面ABCD是梯形,AB∥CD,PD⊥平面ABCD,BD⊥DC,PD=BD=DC=$\frac{1}{2}$AB,E为PC中点.
如图,在四棱锥P-ABCD中,底面ABCD是梯形,AB∥CD,PD⊥平面ABCD,BD⊥DC,PD=BD=DC=$\frac{1}{2}$AB,E为PC中点.