10.已知函数$f(x)=\frac{x}{e^x}$,若不等式f(x)-a(x+1)>0的解集中有且仅有一个整数,则实数a的取值范围是( )
| A. | $[{\frac{1}{e^2},\frac{1}{e}}]$ | B. | $[{\frac{1}{e^2},\frac{1}{e}})$ | C. | $[{\frac{2}{{3{e^2}}},\frac{1}{2e}}]$ | D. | $[{\frac{2}{{3{e^2}}},\frac{1}{2e}})$ |
9.已知由一组样本数据确定的回归直线方程为$\hat y=1.5x+1$,且$\overline x=2$,发现有两组数据(2.6,2.8)与(1.4,5.2)误差较大,去掉这两组数据后,重新求得回归直线的斜率为1.4,那么当x=6时,$\hat y$的估计值为( )
| A. | 9.6 | B. | 10 | C. | 10.6 | D. | 9.4 |
8.下列说法正确的是( )
| A. | 已知命题p,q,若p∨(¬q)为真命题,则q一定是假命题 | |
| B. | 命题“?x∈R,2x>0”的否定是“$?{x_0}∈R,{2^{x_0}}<0$” | |
| C. | “$x=\frac{π}{4}$”是“tan x=l”的充分不必要条件 | |
| D. | “若x1>1,x2>1,则x1+x2>2”的否命题是真命题 |
7.某工厂生产A、B、C三种不同型号的产品,某月生产产品数量之比依次为m:3:2,现用分层抽样方法抽取一个容量为120的样本,已知A种型号产品抽取了45件,则C种型号产品抽取的件数为( )
| A. | 20 | B. | 30 | C. | 40 | D. | 45 |
6.已知复数$z=\frac{2i}{-1+i}$,则( )
| A. | z的实部为1 | B. | |z|=2 | ||
| C. | z的虚部为1 | D. | z的共轭复数为-1-i |
3.某校的学生文娱团队由理科组和文科组构成,具体数据如表所示:
学校准备从该文娱团队中选出4人到某社区参加大型公益活动演出,每选出一名男生,给其所在的组记1分;每选出一名女生,给其所在的组记2分,要求被选出的4人中文科组和理科组的学生都有.
(I)求理科组恰好得4分的概率;
(II)记文科组的得分为X,求随机变量X的分布列和数学期望EX.
0 239233 239241 239247 239251 239257 239259 239263 239269 239271 239277 239283 239287 239289 239293 239299 239301 239307 239311 239313 239317 239319 239323 239325 239327 239328 239329 239331 239332 239333 239335 239337 239341 239343 239347 239349 239353 239359 239361 239367 239371 239373 239377 239383 239389 239391 239397 239401 239403 239409 239413 239419 239427 266669
| 组别 | 文科 | 理科 | ||
| 性别 | 男生 | 女生 | 男生 | 女生 |
| 人数 | 3 | 1 | 3 | 2 |
(I)求理科组恰好得4分的概率;
(II)记文科组的得分为X,求随机变量X的分布列和数学期望EX.
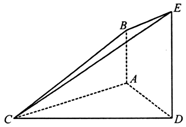 如图,已知AB⊥平面ACD,DE∥AB,△ACD是等腰三角形,∠CAD=120°,AD=DE=2AB.
如图,已知AB⊥平面ACD,DE∥AB,△ACD是等腰三角形,∠CAD=120°,AD=DE=2AB.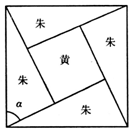 三国时代吴国数学家赵爽所著《周髀算经》中用赵爽弦图给出了勾股定理的绝妙证明,如图是赵爽弦图,图中包含四个全等的勾股形及一个小正方形,分别涂成朱色和黄色,若朱色的勾股形中较大的锐角α为$\frac{π}{3}$,现向该赵爽弦图中随机地投掷一枚飞镖,则飞镖落在黄色的小正方形内的概率为1-$\frac{\sqrt{3}}{2}$.
三国时代吴国数学家赵爽所著《周髀算经》中用赵爽弦图给出了勾股定理的绝妙证明,如图是赵爽弦图,图中包含四个全等的勾股形及一个小正方形,分别涂成朱色和黄色,若朱色的勾股形中较大的锐角α为$\frac{π}{3}$,现向该赵爽弦图中随机地投掷一枚飞镖,则飞镖落在黄色的小正方形内的概率为1-$\frac{\sqrt{3}}{2}$.