题目内容
9.已知由一组样本数据确定的回归直线方程为$\hat y=1.5x+1$,且$\overline x=2$,发现有两组数据(2.6,2.8)与(1.4,5.2)误差较大,去掉这两组数据后,重新求得回归直线的斜率为1.4,那么当x=6时,$\hat y$的估计值为( )| A. | 9.6 | B. | 10 | C. | 10.6 | D. | 9.4 |
分析 由题意求出样本中心点,然后求出新数据的样本中心,利用回归直线的斜率估计值为1.4,求出回归方程,计算x=6时$\hat y$的值.
解答 解:由样本数据点集{(xi,yi)|i=1,2,…,n}求得的回归直线方程为为$\hat y=1.5x+1$,且$\overline{x}$=2,
∴$\overline{y}$=1.5×2+1=4,故数据的样本中心点为(2,4);
去掉(2.6,2.8)与(1.4,5.2),
重新求得的回归直线的斜率估计值为1.4,样本中心点是(2,4),
回归直线方程设为:$\hat y$=1.4x+a,代入(2,4),
求得a=1.2,
∴回归直线l的方程为:$\hat y$=1.4x+1.2,
将x=6代入回归直线方程求得$\hat y$=1.4×6+1.2=9.6.
故选:A.
点评 本题考查了回归直线方程的应用问题,利用回归直线方程恒过样本中心点是关键,属于基础题.

练习册系列答案
相关题目
18.已知函数f(x)=2f(2-x)-x2+5x-5,则曲线y=f(x)在点(1,f(1))处的切线方程为( )
| A. | y=x | B. | y=-2x+3 | C. | y=-3x+4 | D. | y=x-2 |
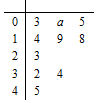 已知函数f(x)=x2+$\sqrt{2}(m-1)x+\frac{m}{4}$,现有一组数据,绘制得到茎叶图,且茎叶图中的数据的平均数为2.(茎叶图中的数据均为小数,其中茎为整数部分,叶为小数部分)
已知函数f(x)=x2+$\sqrt{2}(m-1)x+\frac{m}{4}$,现有一组数据,绘制得到茎叶图,且茎叶图中的数据的平均数为2.(茎叶图中的数据均为小数,其中茎为整数部分,叶为小数部分)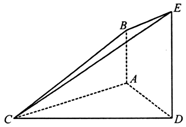 如图,已知AB⊥平面ACD,DE∥AB,△ACD是等腰三角形,∠CAD=120°,AD=DE=2AB.
如图,已知AB⊥平面ACD,DE∥AB,△ACD是等腰三角形,∠CAD=120°,AD=DE=2AB.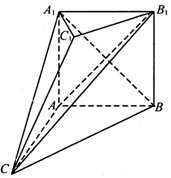 如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,A1C=BC,B1C1∥BC,且${B_1}{C_1}=\frac{1}{2}BC$.
如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,A1C=BC,B1C1∥BC,且${B_1}{C_1}=\frac{1}{2}BC$.