题目内容
1.设$a=\int_0^3{({2x-1})dx}$,则二项式${({x-\frac{a}{2x}})^6}$展开式中x2项的系数为135 (用数字作答).分析 先根据定积分求出a的值,再根据二项式展开式的通项公式求出x2项的系数.
解答 解:$a=\int_0^3{({2x-1})dx}$=(x2-x)|${\;}_{0}^{3}$=9-3=6,
二项式${({x-\frac{a}{2x}})^6}$即(x-$\frac{3}{x}$)6的通项为C6r(-3)r•x6-2r,
令6-2r=2,
解得r=2,
∴展开式中x2项的系数为C62(-3)2=135,
故答案为:135.
点评 本题主要考查二项式定理的应用和定积分的计算,二项式系数的性质,二项式展开式的通项公式,属于基础题.

练习册系列答案
相关题目
12.已知函数f(x)=alnx+x2-(a+2)x恰有两个零点,则实数a的取值范围是( )
| A. | (-1,+∞) | B. | (-2,0) | C. | (-1,0) | D. | (-2,-1) |
6.已知复数$z=\frac{2i}{-1+i}$,则( )
| A. | z的实部为1 | B. | |z|=2 | ||
| C. | z的虚部为1 | D. | z的共轭复数为-1-i |
13.某校高二文科100名学生参加了语数英学科竞赛,年级为了解这些学生语文和数学成绩的情况,将100名学生的语文和数学成绩统计如表:
(I)若数学成绩的优秀率为35%,现利用随机抽样从数学成绩“优秀”的学生中抽取1名学生,求该生语文成绩为“及格”的概率;
(II)在语文成绩为“良”的学生中,已知m≥10,n≥10,求数学成绩“优”比“良”的人数少的概率.
| 语文 | ||||
| 优 | 良 | 及格 | ||
| 数学 | 优 | 13 | m | 5 |
| 良 | 12 | n | 9 | |
| 及格 | 10 | 14 | 7 | |
(II)在语文成绩为“良”的学生中,已知m≥10,n≥10,求数学成绩“优”比“良”的人数少的概率.
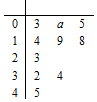 已知函数$f(x)={x^2}+\sqrt{2}(m-1)x+\frac{m}{4}$,现有一组数据(数据量较大),从中随机抽取10个,绘制所得的茎叶图如图所示,且茎叶图中的数据的平均数为2.(茎叶图中的数据均为小数,其中茎为整数部分,叶为小数部分)
已知函数$f(x)={x^2}+\sqrt{2}(m-1)x+\frac{m}{4}$,现有一组数据(数据量较大),从中随机抽取10个,绘制所得的茎叶图如图所示,且茎叶图中的数据的平均数为2.(茎叶图中的数据均为小数,其中茎为整数部分,叶为小数部分)