题目内容
2.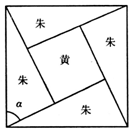 三国时代吴国数学家赵爽所著《周髀算经》中用赵爽弦图给出了勾股定理的绝妙证明,如图是赵爽弦图,图中包含四个全等的勾股形及一个小正方形,分别涂成朱色和黄色,若朱色的勾股形中较大的锐角α为$\frac{π}{3}$,现向该赵爽弦图中随机地投掷一枚飞镖,则飞镖落在黄色的小正方形内的概率为1-$\frac{\sqrt{3}}{2}$.
三国时代吴国数学家赵爽所著《周髀算经》中用赵爽弦图给出了勾股定理的绝妙证明,如图是赵爽弦图,图中包含四个全等的勾股形及一个小正方形,分别涂成朱色和黄色,若朱色的勾股形中较大的锐角α为$\frac{π}{3}$,现向该赵爽弦图中随机地投掷一枚飞镖,则飞镖落在黄色的小正方形内的概率为1-$\frac{\sqrt{3}}{2}$.
分析 利用勾股定理分别求出黄色和朱色面积,利用面积比求概率.
解答 解:设正方形的边长为2,由已知朱色直角三角形一个锐角为$\frac{π}{3}$,得到两条直角边长度分别1、$\sqrt{3}$,所以中心正方形的边长为$\sqrt{3}$-1,面积为($\sqrt{3}$-1)2=4-2$\sqrt{3}$,
由几何概型的公式得到所求概率为$\frac{4-2\sqrt{3}}{4}=1-\frac{\sqrt{3}}{2}$;
故答案为:1-$\frac{\sqrt{3}}{2}$.
点评 本题考查了几何概型的概率求法;关键是明确测度,利用面积比求概率.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
12.(x2+xy+2y)5的展开式中x6y2的系数为( )
| A. | 20 | B. | 40 | C. | 60 | D. | 80 |
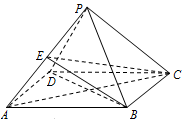 已知四棱锥P-ABCD中,底面ABCD是菱形,∠BAD=60°,AB=PB=PD=2,$PA=\sqrt{6}$.
已知四棱锥P-ABCD中,底面ABCD是菱形,∠BAD=60°,AB=PB=PD=2,$PA=\sqrt{6}$.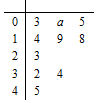 已知函数f(x)=x2+$\sqrt{2}(m-1)x+\frac{m}{4}$,现有一组数据,绘制得到茎叶图,且茎叶图中的数据的平均数为2.(茎叶图中的数据均为小数,其中茎为整数部分,叶为小数部分)
已知函数f(x)=x2+$\sqrt{2}(m-1)x+\frac{m}{4}$,现有一组数据,绘制得到茎叶图,且茎叶图中的数据的平均数为2.(茎叶图中的数据均为小数,其中茎为整数部分,叶为小数部分)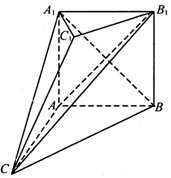 如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,A1C=BC,B1C1∥BC,且${B_1}{C_1}=\frac{1}{2}BC$.
如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,A1C=BC,B1C1∥BC,且${B_1}{C_1}=\frac{1}{2}BC$.