16. 某农科所发现,一种作物的年收获量 y(单位:kg)与它“相近”作物的株数 x具有线性相关关系(所谓两株作物“相近”是指它们的直线距离不超过 1m),并分别记录了相近作物的株数为 1,2,3,5,6,7时,该作物的年收获量的相关数据如表:
某农科所发现,一种作物的年收获量 y(单位:kg)与它“相近”作物的株数 x具有线性相关关系(所谓两株作物“相近”是指它们的直线距离不超过 1m),并分别记录了相近作物的株数为 1,2,3,5,6,7时,该作物的年收获量的相关数据如表:
(1)求该作物的年收获量 y关于它“相近”作物的株数x的线性回归方程;
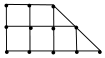
(2)农科所在如图所示的直角梯形地块的每个格点(指纵、横直线的交叉点)处都种了一株该作物,图中
每个小正方形的边长均为 1,若从直角梯形地块的边界和内部各随机选取一株该作物,求这两株作物“相
近”且年产量仅相差3kg的概率.
附:对于一组数据(x1,y1),(x2,y2),…,(xn,yn),其回归直线y=bx+a的斜率和截距的最小二乘估
计分别为,$b=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2}-n{{(\overline x)}^2}}}=\frac{{\sum_{i=1}^n{({x_i}-\overline x)({y_i}-\overline y})}}{{\sum_{i=1}^n{{{({x_i}-\overline x)}^2}}}}$,$a=\overline y-b\overline x$.
 某农科所发现,一种作物的年收获量 y(单位:kg)与它“相近”作物的株数 x具有线性相关关系(所谓两株作物“相近”是指它们的直线距离不超过 1m),并分别记录了相近作物的株数为 1,2,3,5,6,7时,该作物的年收获量的相关数据如表:
某农科所发现,一种作物的年收获量 y(单位:kg)与它“相近”作物的株数 x具有线性相关关系(所谓两株作物“相近”是指它们的直线距离不超过 1m),并分别记录了相近作物的株数为 1,2,3,5,6,7时,该作物的年收获量的相关数据如表:| x | 1 | 2 | 3 | 5 | 6 | 7 |
| y | 60 | 55 | 53 | 46 | 45 | 41 |
(2)农科所在如图所示的直角梯形地块的每个格点(指纵、横直线的交叉点)处都种了一株该作物,图中
每个小正方形的边长均为 1,若从直角梯形地块的边界和内部各随机选取一株该作物,求这两株作物“相
近”且年产量仅相差3kg的概率.
附:对于一组数据(x1,y1),(x2,y2),…,(xn,yn),其回归直线y=bx+a的斜率和截距的最小二乘估
计分别为,$b=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2}-n{{(\overline x)}^2}}}=\frac{{\sum_{i=1}^n{({x_i}-\overline x)({y_i}-\overline y})}}{{\sum_{i=1}^n{{{({x_i}-\overline x)}^2}}}}$,$a=\overline y-b\overline x$.
12.已知函数f(x)=alnx+x2-(a+2)x恰有两个零点,则实数a的取值范围是( )
0 239230 239238 239244 239248 239254 239256 239260 239266 239268 239274 239280 239284 239286 239290 239296 239298 239304 239308 239310 239314 239316 239320 239322 239324 239325 239326 239328 239329 239330 239332 239334 239338 239340 239344 239346 239350 239356 239358 239364 239368 239370 239374 239380 239386 239388 239394 239398 239400 239406 239410 239416 239424 266669
| A. | (-1,+∞) | B. | (-2,0) | C. | (-1,0) | D. | (-2,-1) |
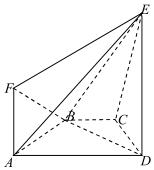 如图所示,等腰梯形ABCD的底角 A等于60°,直角梯形 ADEF所在的平面垂直于平面ABCD,∠EDA=90°,且ED=AD=2AB=2AF.
如图所示,等腰梯形ABCD的底角 A等于60°,直角梯形 ADEF所在的平面垂直于平面ABCD,∠EDA=90°,且ED=AD=2AB=2AF.