Question

20．若正方形ABCD的边长为$2，\overrightarrow{BC}=2\overrightarrow{BE}，\overrightarrow{DC}=λ\overrightarrow{DF}$，若$\overrightarrow{AE}•\overrightarrow{AF}=1$，则λ的值为-4．

Answer 1

分析 作出图形，依题意得：$\overrightarrow{AE}$=$\frac{1}{2}$$\overrightarrow{BC}$-$\overrightarrow{BA}$，$\overrightarrow{AF}$=$\overrightarrow{BC}$-$\frac{1}{λ}$$\overrightarrow{BA}$，于是$\overrightarrow{AE}•\overrightarrow{AF}$=（$\frac{1}{2}$$\overrightarrow{BC}$-$\overrightarrow{BA}$）•（$\overrightarrow{BC}$-$\frac{1}{λ}$$\overrightarrow{BA}$）=$\frac{1}{2}$${\overrightarrow{BC}}^{2}$+$\frac{1}{λ}$${\overrightarrow{BA}}^{2}$=$\frac{1}{2}$×4+$\frac{4}{λ}$=1，可解得λ的值．

解答 解：∵正方形ABCD的边长为$2，\overrightarrow{BC}=2\overrightarrow{BE}，\overrightarrow{DC}=λ\overrightarrow{DF}$，作图如下：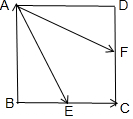

∴$\overrightarrow{AE}$=$\overrightarrow{BE}$-$\overrightarrow{BA}$=$\frac{1}{2}$$\overrightarrow{BC}$-$\overrightarrow{BA}$，
$\overrightarrow{AF}$=$\overrightarrow{AD}$+$\overrightarrow{DF}$=$\overrightarrow{BC}$+$\frac{1}{λ}$$\overrightarrow{DC}$=$\overrightarrow{BC}$-$\frac{1}{λ}$$\overrightarrow{BA}$，
∴$\overrightarrow{AE}•\overrightarrow{AF}$=（$\frac{1}{2}$$\overrightarrow{BC}$-$\overrightarrow{BA}$）•（$\overrightarrow{BC}$-$\frac{1}{λ}$$\overrightarrow{BA}$）=$\frac{1}{2}$${\overrightarrow{BC}}^{2}$+$\frac{1}{λ}$${\overrightarrow{BA}}^{2}$=$\frac{1}{2}$×4+$\frac{4}{λ}$=1，
解得：λ=-4，
故答案为：-4．

点评 本题考查平面向量数量积的运算，考查平面向量基本定理的应用，考查作图能力与运算能力，属于中档题．