题目内容
18.已知函数$f(x)=\frac{{{x^2}-1}}{{lnx-a{x^2}}}(a∈$R).(1)当a=0时,求函数 f(x)的单调区间;
(2)若对于任意x∈(1,e),不等式f(x)>1恒成立,求 a的取值范围.
分析 (1)当a=0时,$f(x)=\frac{{{x^2}-1}}{lnx}(x>0$且$x≠1),f'(x)=\frac{{2xlnx-x+\frac{1}{x}}}{{{{ln}^2}x}}$,令$g(x)=2xlnx-x+\frac{1}{x},g'(x)=2lnx+\frac{{{x^2}-1}}{x^2}$,利用导数性质能求出函数 f(x)的单调区间.
(2)问题等价于$\left\{\begin{array}{l}lnx-a{x^2}>0\\{x^2}-1>lnx-a{x^2}\end{array}\right.$对于任意 x∈(1,e)恒成立,$lnx-a{x^2}>0?a<\frac{lnx}{x^2}$,由此能求出a的取值范围.
解答 解:(1)当a=0时,$f(x)=\frac{{{x^2}-1}}{lnx}(x>0$且$x≠1),f'(x)=\frac{{2xlnx-x+\frac{1}{x}}}{{{{ln}^2}x}}$,
令$g(x)=2xlnx-x+\frac{1}{x},g'(x)=2lnx+\frac{{{x^2}-1}}{x^2}$,
当x∈(0,1)时,g'(x)<0,
当x∈(1,+∞)时,g'(x)>0,
∴函数g(x)在 (0,1)上单调递减,在 (1,+∞)上单调递增,
∴当x>0且x≠1时,g(x)>g(1)=0,f'(x)>0,
∴函数f(x)在 (0,1)上单调递增,在 (1,+∞)上单调递增.
(2)∵x∈(1,e),∴x2-1>0,
∴问题等价于$\left\{\begin{array}{l}lnx-a{x^2}>0\\{x^2}-1>lnx-a{x^2}\end{array}\right.$对于任意 x∈(1,e)恒成立,
$lnx-a{x^2}>0?a<\frac{lnx}{x^2}$,
令$h(x)=\frac{lnx}{x^2},h'(x)=\frac{1-2lnx}{x^3},h'(x)>0?1<x<\sqrt{e};h'(x)<0?\sqrt{e}<x<e$,
∴h(x)在$({1,\sqrt{e}})$上单调递增,在 $({\sqrt{e},e})$上单调递减,
∴$h(x)∈({0,\frac{1}{2e}}]$,∴a≤0,${x^2}-1>lnx-a{x^2}?a>\frac{{lnx-{x^2}+1}}{x^2}$,
令$φ(x)=\frac{{lnx-{x^2}+1}}{x^2},φ'(x)=\frac{-1-2lnx}{x^3}<0$,
∴φ(x)在$({1,\sqrt{e}})$上单递减,∴$φ(x)∈({\frac{2}{e^2}-1,0})$,
∴a≥0,综上所述,a的取值范围为{0}.
点评 本题考查函数的单调区间的求法,考查实数的取值范围的求法,考查导数的性质及应用等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、分类与整合思想,是中档题.

| A. | {x|x≥-2} | B. | {x|x>-2} | C. | {x|1<x<3} | D. | {x|1<x≤3} |
| A. | -i | B. | i | C. | $\frac{4}{5}-i$ | D. | $\frac{4}{5}-\frac{3}{5}i$ |
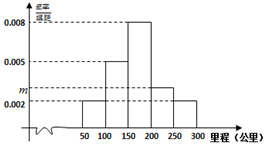 绿色出行越来越受到社会的关注,越来越多的消费者对新能源汽车感兴趣.但是消费者比较关心的问题是汽车的续驶里程.某研究小组从汽车市场上随机抽取20辆纯电动汽车调查其续驶里程(单次充电后能行驶的最大里程),被调查汽车的续驶里程全部介于50公里和300公里之间,将统计结果分成5组:[50,100),[100,150),[150,200),[200,250),[250,300],绘制成如图所示的频率分布直方图.
绿色出行越来越受到社会的关注,越来越多的消费者对新能源汽车感兴趣.但是消费者比较关心的问题是汽车的续驶里程.某研究小组从汽车市场上随机抽取20辆纯电动汽车调查其续驶里程(单次充电后能行驶的最大里程),被调查汽车的续驶里程全部介于50公里和300公里之间,将统计结果分成5组:[50,100),[100,150),[150,200),[200,250),[250,300],绘制成如图所示的频率分布直方图.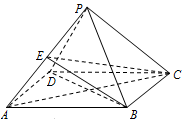 已知四棱锥P-ABCD中,底面ABCD是菱形,∠BAD=60°,AB=PB=PD=2,$PA=\sqrt{6}$.
已知四棱锥P-ABCD中,底面ABCD是菱形,∠BAD=60°,AB=PB=PD=2,$PA=\sqrt{6}$.