8.若函数$f(x)=\frac{{{a^x}-1}}{{{a^x}+1}}+$${log_a}({\frac{1-x}{1+x}})$(a>0,a≠1),f(m)=n,m∈(-1,1),则f(-m)=( )
| A. | n | B. | -n | C. | 0 | D. | 不存在 |
6.为调查高中生的数学成绩与学生自主学习时间之间的相关关系,某重点高中数学教师对新入学的45名学生进行了跟踪调查,其中每周自主做数学题的时间不少于15小时的有19人,余下的人中,在高三模拟考试中数学平均成绩不足120分的占$\frac{8}{13}$,统计成绩后,得到如下的2×2列联表:
(Ⅰ)请完成上面的2×2列联表,并判断能否在犯错误的概率不超过0.01的前提下认为“高中生的数学成绩与学生自主学习时间有关”;
(Ⅱ)( i) 按照分层抽样的方法,在上述样本中,从分数大于等于120分和分数不足120分的两组学生中抽取9名学生,设抽到的不足120分且周做题时间不足15小时的人数是X,求X的分布列(概率用组合数算式表示);
( ii) 若将频率视为概率,从全校大于等于120分的学生中随机抽取20人,求这些人中周做题时间不少于15小时的人数的期望和方差.
附:${K^2}=\frac{{n{{(ad-bc)}^2}}}{{({a+b})({c+d})({a+c})({b+d})}}$
| 分数大于等于120分 | 分数不足120分 | 合 计 | |
| 周做题时间不少于15小时 | 15 | 4 | 19 |
| 周做题时间不足15小时 | 10 | 16 | 26 |
| 合 计 | 25 | 20 | 45 |
(Ⅱ)( i) 按照分层抽样的方法,在上述样本中,从分数大于等于120分和分数不足120分的两组学生中抽取9名学生,设抽到的不足120分且周做题时间不足15小时的人数是X,求X的分布列(概率用组合数算式表示);
( ii) 若将频率视为概率,从全校大于等于120分的学生中随机抽取20人,求这些人中周做题时间不少于15小时的人数的期望和方差.
附:${K^2}=\frac{{n{{(ad-bc)}^2}}}{{({a+b})({c+d})({a+c})({b+d})}}$
| P(K2≥k0) | 0.050 | 0.010 | 0.001 |
| k0 | 3.841 | 6.635 | 10.828 |
4.一条光线从点(1,-1)射出,经y轴反射后与圆(x-2)2+y2=1相交,则入射光线所在直线的斜率的取值范围为( )
| A. | $[{-\frac{3}{4},0}]$ | B. | $[{0,\frac{3}{4}}]$ | C. | $({-\frac{3}{4},0})$ | D. | $({0,\frac{3}{4}})$ |
3.已知P为圆C:x2+y2=π2内任意一点,则点P落在函数f(x)=sinx的图象与x轴围成的封闭区域内的概率为( )
| A. | 0 | B. | 1 | C. | $\frac{2}{π^3}$ | D. | $\frac{4}{π^3}$ |
1.已知Rt△ABC,AB=3,BC=4,CA=5,P为△ABC外接圆上的一动点,且$\overrightarrow{AP}=x\overrightarrow{AB}+y\overrightarrow{AC},则x+y$的最大值是( )
0 239225 239233 239239 239243 239249 239251 239255 239261 239263 239269 239275 239279 239281 239285 239291 239293 239299 239303 239305 239309 239311 239315 239317 239319 239320 239321 239323 239324 239325 239327 239329 239333 239335 239339 239341 239345 239351 239353 239359 239363 239365 239369 239375 239381 239383 239389 239393 239395 239401 239405 239411 239419 266669
| A. | $\frac{5}{4}$ | B. | $\frac{4}{3}$ | C. | $\frac{{\sqrt{17}}}{6}$ | D. | $\frac{5}{3}$ |
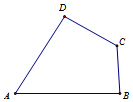 如图,A,B,C,D为平面四边形ABCD的四个内角,若A+C=180°,AB=6,BC=4,CD=5,AD=5,则四边形ABCD面积是10$\sqrt{6}$.
如图,A,B,C,D为平面四边形ABCD的四个内角,若A+C=180°,AB=6,BC=4,CD=5,AD=5,则四边形ABCD面积是10$\sqrt{6}$.