题目内容
4.一条光线从点(1,-1)射出,经y轴反射后与圆(x-2)2+y2=1相交,则入射光线所在直线的斜率的取值范围为( )| A. | $[{-\frac{3}{4},0}]$ | B. | $[{0,\frac{3}{4}}]$ | C. | $({-\frac{3}{4},0})$ | D. | $({0,\frac{3}{4}})$ |
分析 如图所示,由题意可设入射光线PQ的方程为:y+1=k(x-1),可得Q(0,-1-k).反射光线QAB的方程为:y=-kx-1-k.利用直线与圆相交可得$\frac{|-2k-1-k|}{\sqrt{1+{k}^{2}}}$<1,解出即可得出.
解答 解:如图所示,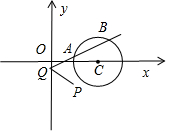
由题意可设入射光线PQ的方程为:y+1=k(x-1),
令x=0,则y=-1-k,可得Q(0,-1-k).
反射光线QAB的方程为:y=-kx-1-k.
则$\frac{|-2k-1-k|}{\sqrt{1+{k}^{2}}}$<1,解得:$-\frac{3}{4}<k<0$.
∴入射光线所在直线的斜率的取值范围为$(-\frac{3}{4},0)$.
故选:C.
点评 本题考查了入射光线与反射光线的性质、对称性、直线与圆的位置关系、点到直线的距离公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
8.已知集合A={x|2x>1},B={x||x|<3},则A∩B=( )
| A. | (-3,0) | B. | (-3,3) | C. | (0,3) | D. | (0,+∞) |
16.(x2+ax-1)6的展开式中x2的系数为54,则实数a为( )
| A. | -2 | B. | -3或3 | C. | -2或2 | D. | -3或-2 |
 如图,在直三棱柱ABC-A1B1C1中,△ABC是正三角形,E是棱BB1的中点.
如图,在直三棱柱ABC-A1B1C1中,△ABC是正三角形,E是棱BB1的中点.