19.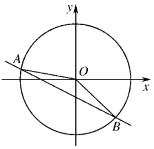 如图,直线x+2y=a与圆x2+y2=1相交于不同的两点A(x1,y1),B(x2,y2),O为坐标原点,若$\overrightarrow{OA}$•$\overrightarrow{OB}$=a,则实数a的值为( )
如图,直线x+2y=a与圆x2+y2=1相交于不同的两点A(x1,y1),B(x2,y2),O为坐标原点,若$\overrightarrow{OA}$•$\overrightarrow{OB}$=a,则实数a的值为( )
 如图,直线x+2y=a与圆x2+y2=1相交于不同的两点A(x1,y1),B(x2,y2),O为坐标原点,若$\overrightarrow{OA}$•$\overrightarrow{OB}$=a,则实数a的值为( )
如图,直线x+2y=a与圆x2+y2=1相交于不同的两点A(x1,y1),B(x2,y2),O为坐标原点,若$\overrightarrow{OA}$•$\overrightarrow{OB}$=a,则实数a的值为( )| A. | $\frac{5-\sqrt{65}}{4}$ | B. | $\frac{\sqrt{65}-5}{4}$ | C. | $\frac{5-\sqrt{55}}{4}$ | D. | $\frac{\sqrt{55}-5}{4}$ |
17.一汽车厂生产A,B,C三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如表(单位:辆):
按类用分层抽样的方法在这个月生产的轿车中抽取50辆,其中有A类轿车10辆.
(Ⅰ)求z的值;
(Ⅱ)用分层抽样的方法在C类轿车中抽取一个容量为5的样本.将该样本看成一个总体,从中任取2辆,求至少有1辆舒适型轿车的概率;
(Ⅲ)用随机抽样的方法从B类舒适型轿车中抽取8辆,经检测它们的得分x的值如下:9.4,8.6,9.2,9.6,8.7,9.3,9.0,8.2,把这8辆轿车的得分看成一个总体,从中任取一个数xi(1≤i≤8,i∈N),设样本平均数为$\overline{x}$,求|xi-$\overline{x}$|≤0.5的概率.
| 轿车A | 轿车B | 轿车C | |
| 舒适型 | 100 | 150 | z |
| 标准型 | 300 | 450 | 600 |
(Ⅰ)求z的值;
(Ⅱ)用分层抽样的方法在C类轿车中抽取一个容量为5的样本.将该样本看成一个总体,从中任取2辆,求至少有1辆舒适型轿车的概率;
(Ⅲ)用随机抽样的方法从B类舒适型轿车中抽取8辆,经检测它们的得分x的值如下:9.4,8.6,9.2,9.6,8.7,9.3,9.0,8.2,把这8辆轿车的得分看成一个总体,从中任取一个数xi(1≤i≤8,i∈N),设样本平均数为$\overline{x}$,求|xi-$\overline{x}$|≤0.5的概率.
14.设函数f(x)=(x-a)2+(ln x2-2a)2,其中x>0,a∈R,存在x0使得f(x0)≤b成立,则实数b的最小值为( )
0 239201 239209 239215 239219 239225 239227 239231 239237 239239 239245 239251 239255 239257 239261 239267 239269 239275 239279 239281 239285 239287 239291 239293 239295 239296 239297 239299 239300 239301 239303 239305 239309 239311 239315 239317 239321 239327 239329 239335 239339 239341 239345 239351 239357 239359 239365 239369 239371 239377 239381 239387 239395 266669
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{4}{5}$ | D. | 1 |
 如图所示的几何体ABCDE,EA⊥平面ABC,EA∥DC,AB⊥AC,EA=AB=AC=2DC,M是线段BD上的动点.
如图所示的几何体ABCDE,EA⊥平面ABC,EA∥DC,AB⊥AC,EA=AB=AC=2DC,M是线段BD上的动点.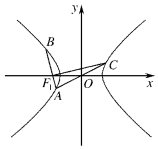 如图,过双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a,b>0)左焦点F1的直线交双曲线左支于A,B两点,C是双曲线右支上一点,且A,C在x轴的异侧,若满足|OA|=|OF1|=|OC|,|CF1|=2|BF1|,则双曲线的离心率为$\frac{\sqrt{17}}{3}$.
如图,过双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a,b>0)左焦点F1的直线交双曲线左支于A,B两点,C是双曲线右支上一点,且A,C在x轴的异侧,若满足|OA|=|OF1|=|OC|,|CF1|=2|BF1|,则双曲线的离心率为$\frac{\sqrt{17}}{3}$.