题目内容
1.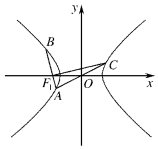 如图,过双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a,b>0)左焦点F1的直线交双曲线左支于A,B两点,C是双曲线右支上一点,且A,C在x轴的异侧,若满足|OA|=|OF1|=|OC|,|CF1|=2|BF1|,则双曲线的离心率为$\frac{\sqrt{17}}{3}$.
如图,过双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a,b>0)左焦点F1的直线交双曲线左支于A,B两点,C是双曲线右支上一点,且A,C在x轴的异侧,若满足|OA|=|OF1|=|OC|,|CF1|=2|BF1|,则双曲线的离心率为$\frac{\sqrt{17}}{3}$.
分析 取双曲线的右焦点F2,连接CF2,延长交双曲线于D,连接AF2,DF1,由平面几何的性质可得四边形F1AF2C为矩形,设|CF1|=2|BF1|=2m,运用双曲线的定义和对称性,结合勾股定理,化简可得3m=4a,代入方程结合离心率公式,即可得到所求.
解答  解:取双曲线的右焦点F2,连接CF2,延长交双曲线于D,
解:取双曲线的右焦点F2,连接CF2,延长交双曲线于D,
连接AF2,DF1,
由|OA|=|OF1|=|OC|=|OF2|=c,
可得四边形F1AF2C为矩形,
设|CF1|=2|BF1|=2m,
由对称性可得|DF2|=m,|AF1|=$\sqrt{4{c}^{2}-4{m}^{2}}$,
即有|CF2|=$\sqrt{4{c}^{2}-4{m}^{2}}$,
由双曲线的定义可得2a=|CF1|-|CF2|=2m-$\sqrt{4{c}^{2}-4{m}^{2}}$,①
在直角三角形DCF1中,|DC|=m+$\sqrt{4{c}^{2}-4{m}^{2}}$,|CF1|=2m,
|DF1|=2a+m,
可得(2a+m)2=(2m)2+(m+$\sqrt{4{c}^{2}-4{m}^{2}}$)2,②
由①②可得3m=4a,即m=$\frac{4a}{3}$,
代入①可得,2a=$\frac{8a}{3}$-$\sqrt{4{c}^{2}-\frac{64{a}^{2}}{9}}$,
化简可得c2=$\frac{17}{9}$a2,
即有e=$\frac{c}{a}$=$\frac{\sqrt{17}}{3}$.
故答案为:$\frac{\sqrt{17}}{3}$.
点评 本题考查双曲线的离心率的求法,注意运用双曲线的定义和平面几何的性质,主要是勾股定理的运用,考查化简整理的运算能力,属于中档题.

练习册系列答案
相关题目
12.设x1,x2为f(x)=sin(ωx-$\frac{π}{6}$)(ω>0)的两个零点,且|x2-x1|的最小值为1,则ω=( )
| A. | π | B. | $\frac{π}{2}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{4}$ |
13.复数$z=|{({\sqrt{3}-i})i}|+{i^{2017}}$(i为虚数单位),则复数z的共轭复数为( )
| A. | 2-i | B. | 2+i | C. | 4-i | D. | 4+i |
10.椭圆$C:\frac{x^2}{4}+\frac{y^2}{3}=1$与双曲线$E:\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a,b>0)$有相同的焦点,且两曲线的离心率互为倒数,则双曲线渐近线的倾斜角的正弦值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
11.过点P(1,-3)的直线既与抛物线y=x2相切,又与圆(x-2)2+y2=5相切,则切线的斜率为( )
| A. | -6 | B. | -2 | C. | -1 | D. | 3 |

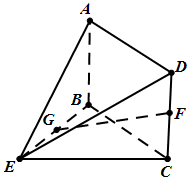 如图,在几何体ABCDE中,四边形ABCD是矩形,AB⊥平面BCE,BE⊥CE,AB=BE=EC=2,G,F分别是线段BE,DC的中点.
如图,在几何体ABCDE中,四边形ABCD是矩形,AB⊥平面BCE,BE⊥CE,AB=BE=EC=2,G,F分别是线段BE,DC的中点.