7.数列{an}的前n项和为Sn,a1=1,${a_n}+{a_{n+1}}=3×{2^{n-1}}$,则S2017=( )
| A. | 22018-1 | B. | 22018+1 | C. | 22017-1 | D. | 22017+1 |
6.已知直线$\sqrt{3}x-y-\sqrt{3}=0$与抛物线y2=4x交于A,B两点(A在x轴上方),与x轴交于F点,$\overrightarrow{OF}=λ\overrightarrow{OA}+μ\overrightarrow{OB}$,则λ-μ=( )
| A. | $\frac{1}{2}$ | B. | $-\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $-\frac{1}{3}$ |
5.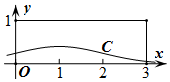 在如图所示的矩形中随机投掷30000个点,则落在曲线C下方(曲线C为正态分布N(1,1)的正态曲线)的点的个数的估计值为( )
在如图所示的矩形中随机投掷30000个点,则落在曲线C下方(曲线C为正态分布N(1,1)的正态曲线)的点的个数的估计值为( )
附:正态变量在区间(μ-σ,μ+σ),(μ-2σ,μ+2σ),(μ-3σ,μ+3σ)内取值的概率分别是0.683,0.954,0.997.
 在如图所示的矩形中随机投掷30000个点,则落在曲线C下方(曲线C为正态分布N(1,1)的正态曲线)的点的个数的估计值为( )
在如图所示的矩形中随机投掷30000个点,则落在曲线C下方(曲线C为正态分布N(1,1)的正态曲线)的点的个数的估计值为( )附:正态变量在区间(μ-σ,μ+σ),(μ-2σ,μ+2σ),(μ-3σ,μ+3σ)内取值的概率分别是0.683,0.954,0.997.
| A. | 4985 | B. | 8185 | C. | 9970 | D. | 24555 |
4.若$sinα+3sin(\frac{π}{2}+α)=0$,则cos2α的值为( )
| A. | $-\frac{3}{5}$ | B. | $\frac{3}{5}$ | C. | $-\frac{4}{5}$ | D. | $\frac{4}{5}$ |
3.已知双曲线$\frac{x^2}{9}-\frac{y^2}{4}=1$,则其焦距为( )
| A. | $\sqrt{5}$ | B. | $2\sqrt{5}$ | C. | $\sqrt{13}$ | D. | $2\sqrt{13}$ |
2.设点P(x,y)在不等式组$\left\{\begin{array}{l}x≥1\\ 2x-y≤0\\ x+y-6≤0\end{array}\right.$所表示的平面区域内,则$z=\frac{9xy}{{9{x^2}+{y^2}}}$的取值范围为( )
| A. | $[{\frac{18}{13},\frac{3}{2}}]$ | B. | $[{\frac{45}{34},\frac{3}{2}}]$ | C. | $[{\frac{45}{34},\frac{18}{13}}]$ | D. | $[{\frac{18}{13},\frac{45}{34}}]$ |
1.设函数f(x)=(x-2)n,其中$n=4\int_{-π}^{2π}{sin({x+π})dx}$,则f(x)的展开式中含x6的项的系数为( )
| A. | -112 | B. | -56 | C. | 112 | D. | 56 |
20.已知数列{an}的前 n项和记为 Sn,满足${a_1}=5,{a_7}=\frac{8}{3}$,且2an+1=an+an+2,要使得Sn取到最大值,则n=( )
0 239191 239199 239205 239209 239215 239217 239221 239227 239229 239235 239241 239245 239247 239251 239257 239259 239265 239269 239271 239275 239277 239281 239283 239285 239286 239287 239289 239290 239291 239293 239295 239299 239301 239305 239307 239311 239317 239319 239325 239329 239331 239335 239341 239347 239349 239355 239359 239361 239367 239371 239377 239385 266669
| A. | 13 | B. | 14 | C. | 15或16 | D. | 16 |