题目内容

3．已知双曲线$\frac{x^2}{9}-\frac{y^2}{4}=1$，则其焦距为（　　）
A．$\sqrt{5}$B．$2\sqrt{5}$C．$\sqrt{13}$D．$2\sqrt{13}$

分析 直接利用双曲线方程求解双曲线的焦距即可．

解答 解：双曲线$\frac{x^2}{9}-\frac{y^2}{4}=1$，则其焦距为：2$\sqrt{9+4}$=2$\sqrt{13}$．
故选：D．

点评 本题考查双曲线的简单性质的应用，考查计算能力．

练习册系列答案
相关题目
13．已知点P（x，y）在不等式组$\left\{\begin{array}{l}2x-y+a≥0\\ 3x+y-3≤0\end{array}\right.$（a为常数）表示的平面区域上运动，若z=4x+3y的最大值为8，则a=2．
14．已知函数f（x）=（a+1）lnx-x2，$g（x）=\frac{{{x^2}+a}}{x}$．
（Ⅰ）讨论函数f（x）的单调区间；
（Ⅱ）若函数f（x）与g（x）在（0，+∞）上的单调性正好相反．
（1）对于$?{x_1}，{x_2}∈[\frac{1}{e}，3]$，不等式$\frac{1}{{f（{x_1}）-g（{x_2}）}}≤\frac{1}{t-1}$恒成立，求实数t的取值范围；
（2）令h（x）=xg（x）-f（x），两正实数x1、x2满足h（x1）+h（x2）+6x1x2=6，证明0＜x1+x2≤1．
11．已知正项数列{an}的首项a1=1，前n项和为Sn，若以（an，Sn）为坐标的点在曲线y=$\frac{1}{2}$x（x+1）上，则数列{an}的通项公式为an=n．
18．若集合M={y|y=x4，x∈（-1，0）}，集合$N=\left\{{x|y=ln\frac{x}{x-1}}\right\}$，则下列各式中正确的是（　　）
A．M?NB．N?MC．M∩N=ϕD．M=N
8．已知函数f（x）=ln（1+x）-ln（1-x），给出以下四个命题：
①?x∈（-1，1），有f（-x）=-f（x）；
②?x1，x2∈（-1，1）且x1≠x2，有$\frac{{f（{x_1}）-f（{x_2}）}}{{{x_1}-{x_2}}}＞0$；
③?x1，x2∈（0，1），有$f（\frac{{{x_1}+{x_2}}}{2}）≤\frac{{f（{x_1}）+f（{x_2}）}}{2}$；
④?x∈（-1，1），|f（x）|≥2|x|．
其中所有真命题的序号是（　　）
A．①②B．③④C．①②③D．①②③④
15．定义在R上的奇函数f（x）在（-∞，0）上递增，f（2）=1，则满足|f（log${\;}_{\frac{1}{2}}$x）|＞1的x的取值范围是（　　）
A．（$\frac{1}{4}$，4）B．（0，$\frac{1}{2}$）C．（0，$\frac{1}{2}$）∪（2，+∞）D．（0，$\frac{1}{4}$）∪（4，+∞）
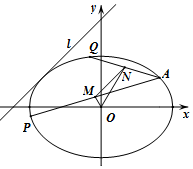12．已知椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$（a＞b＞0）的离心率$e=\frac{{\sqrt{2}}}{2}$，且与直线l：y=x+3相切．
（Ⅰ）求椭圆的标准方程；
（Ⅱ）过椭圆上点A（2，1）作椭圆的弦AP，AQ，若AP，AQ的中点分别为M，N，若MN平行于l，则OM，ON斜率之和是否为定值？
7．变量x，y满足约束条件$\left\{\begin{array}{l}{x-y+1≥0}\\{x+2y-4≥0}\\{3x+y-6≤0}\end{array}\right.$，z=ax+y（a＜0）的最大值为$\frac{3}{2}$，则a=-$\frac{3}{5}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网