题目内容
9.已知点$P(x,y)满足\left\{\begin{array}{l}x+y≥4\\ y≤x+2\\ x≤3\end{array}\right.$,点A,B是圆x2+y2=2上的两个点,则∠APB的最大值为$\frac{π}{3}$.分析 由题意知点P在不等式$\left\{\begin{array}{l}{x+y≥4}\\{y≤x+2}\\{x≤3}\end{array}\right.$表示的平面区域内(包含边界)运动,
当P位于圆x2+y2=2外时,若∠APB最大,则PA,PB所在直线与圆相切,
且点P位于离圆心最近的H处;由此求出∠APB的最大值.
解答  解:由已知可得点P在不等式组$\left\{\begin{array}{l}{x+y≥4}\\{y≤x+2}\\{x≤3}\end{array}\right.$表示的平面如图所示(包含边界)运动,
解:由已知可得点P在不等式组$\left\{\begin{array}{l}{x+y≥4}\\{y≤x+2}\\{x≤3}\end{array}\right.$表示的平面如图所示(包含边界)运动,
易知点P位于圆x2+y2=2外时,∠APB最大时,
当PA,PB所在直线与圆相切,且点P位于离圆心最近的H处;
此时,圆心到直线x+y-4=0的距离为$|OH|=2\sqrt{2}$,
所以在Rt△OAP中|OP|=2|OA|,
所以$∠OPA=\frac{π}{6}$,
同理$∠OPB=\frac{π}{6}$,
此时$∠APB=\frac{π}{3}$.
故答案为:$\frac{π}{3}$.
点评 本题考查了线性规划的应用问题,也考查了数形结合的应用思想,是综合题.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
20.已知a=5log33.4,b=5log33.6,c=($\frac{1}{5}$)log30.5,则a,b,c的大小关系是( )
| A. | c>a>b | B. | b>a>c | C. | a>b>c | D. | a>c>b |
17.若z=(2+i)cosπ(i为虚数单位),则z=( )
| A. | 2+i | B. | $\frac{2-i}{5}$ | C. | $\frac{2-i}{3}$ | D. | 1 |
4.若$sinα+3sin(\frac{π}{2}+α)=0$,则cos2α的值为( )
| A. | $-\frac{3}{5}$ | B. | $\frac{3}{5}$ | C. | $-\frac{4}{5}$ | D. | $\frac{4}{5}$ |
14.一个由底面是正三角形的三棱柱和三棱锥组成的组合体,其三视图如图所示,则该组合体的体积为( )
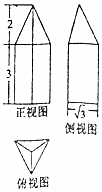

| A. | $\frac{11\sqrt{3}}{3}$ | B. | $\frac{15\sqrt{3}}{4}$ | C. | $\frac{11\sqrt{3}}{4}$ | D. | 5$\sqrt{3}$ |
1.已知函数f(x)=sinx+cosx,g(x)=2cosx,动直线x=t与f(x)和g(x)的图象分别交于A、B两点,则|AB|的取值范围是( )
| A. | [0,1] | B. | [0,$\sqrt{2}$] | C. | [0,2] | D. | [1,$\sqrt{2}$] |
18.已知平面向量$\vec a=({1,2}),\vec b=({-2,m})$,且$\vec a∥\vec b$,则$|{\vec b}|$为( )
| A. | 2$\sqrt{5}$ | B. | $\sqrt{5}$ | C. | 3$\sqrt{5}$ | D. | 1 |
13.若定义在(0,1)上的函数f(x)满足:f(x)>0且对任意的x∈(0,1),有f($\frac{2x}{1+{x}^{2}}$)=2f(x).则( )
| A. | 对任意的正数M,存在x∈(0,1),使f(x)≥M | |
| B. | 存在正数M,对任意的x∈(0,1),使f(x)≤M | |
| C. | 对任意的x1,x2∈(0,1)且x1<x2,有f(x1)<f(x2) | |
| D. | 对任意的x1,x2∈(0,1)且x1<x2,有f(x1)>f(x2) |