题目内容
2.设点P(x,y)在不等式组$\left\{\begin{array}{l}x≥1\\ 2x-y≤0\\ x+y-6≤0\end{array}\right.$所表示的平面区域内,则$z=\frac{9xy}{{9{x^2}+{y^2}}}$的取值范围为( )| A. | $[{\frac{18}{13},\frac{3}{2}}]$ | B. | $[{\frac{45}{34},\frac{3}{2}}]$ | C. | $[{\frac{45}{34},\frac{18}{13}}]$ | D. | $[{\frac{18}{13},\frac{45}{34}}]$ |
分析 画出不等式组$\left\{\begin{array}{l}x≥1\\ 2x-y≤0\\ x+y-6≤0\end{array}\right.$表示的平面区域,化$z=\frac{9xy}{{9{x^2}+{y^2}}}$=$\frac{9(\frac{y}{x})}{9{+(\frac{y}{x})}^{2}}$,设t=$\frac{y}{x}$,利用斜率求出t的取值范围,再利用基本不等式求出z的取值范围.
解答 解:画出不等式组$\left\{\begin{array}{l}x≥1\\ 2x-y≤0\\ x+y-6≤0\end{array}\right.$所表示的平面区域内如图所示,
由$\left\{\begin{array}{l}{x=1}\\{x+y-6=0}\end{array}\right.$求出点A(1,5);
又$z=\frac{9xy}{{9{x^2}+{y^2}}}$=$\frac{9(\frac{y}{x})}{9{+(\frac{y}{x})}^{2}}$,
设t=$\frac{y}{x}$,则kBC≤t≤kOA,即2≤t≤5,
∴z=$\frac{9t}{9{+t}^{2}}$=$\frac{9}{\frac{9}{t}+t}$;
又2≤t≤5,
∴2•$\sqrt{\frac{9}{t}•t}$≤$\frac{9}{t}$+t≤$\frac{9}{5}$+5,
即6≤$\frac{9}{t}$+t≤$\frac{34}{5}$,
∴$\frac{45}{34}$≤$\frac{9}{\frac{9}{t}+t}$≤$\frac{3}{2}$,
即z的取值范围是[$\frac{45}{34}$,$\frac{3}{2}$].
故选:B.
点评 本题考查了二元一次不等式组表示平面区域的应用问题,也考查了转化思想的应用问题,是综合题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 2+i | B. | $\frac{2-i}{5}$ | C. | $\frac{2-i}{3}$ | D. | 1 |
| A. | 22018-1 | B. | 22018+1 | C. | 22017-1 | D. | 22017+1 |
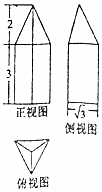
| A. | $\frac{11\sqrt{3}}{3}$ | B. | $\frac{15\sqrt{3}}{4}$ | C. | $\frac{11\sqrt{3}}{4}$ | D. | 5$\sqrt{3}$ |
 以下茎叶图记录了某学习小组六名同学在一次数学测试中的成绩(单位:分),已知该组数据的中位数为85,则x的值为8.
以下茎叶图记录了某学习小组六名同学在一次数学测试中的成绩(单位:分),已知该组数据的中位数为85,则x的值为8.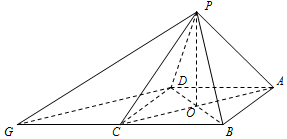 在四棱锥P-ABCD中,底面ABCD为菱形,∠PAD=∠PAB,AC交BD于O,
在四棱锥P-ABCD中,底面ABCD为菱形,∠PAD=∠PAB,AC交BD于O,