题目内容
4.若$sinα+3sin(\frac{π}{2}+α)=0$,则cos2α的值为( )| A. | $-\frac{3}{5}$ | B. | $\frac{3}{5}$ | C. | $-\frac{4}{5}$ | D. | $\frac{4}{5}$ |
分析 根据诱导公式化简,结合同角三角函数关系式和万能公式即可求解cos2α的值.
解答 解:由$sinα+3sin(\frac{π}{2}+α)=0$,
则sinα+3cosα=0,
可得:tanα=$\frac{sinα}{cosα}$=-3;
则cos2α=cos2α-sin2α=$\frac{1-ta{n}^{2}α}{ta{n}^{2}α+1}$=$\frac{1-9}{1+9}=-\frac{4}{5}$.
故选:C
点评 本题考查了诱导公式化简能力和同角三角函数关系式,万能公式的应用,属于基础题.

练习册系列答案
相关题目
19.设点F是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的右焦点,点F到渐近线的距离与双曲线的焦距之比为1:4,则双曲线的渐近线方程为( )
| A. | $\sqrt{3}x±y=0$ | B. | $x±\sqrt{3}y=0$ | C. | $\sqrt{15}x±y=0$ | D. | $x±\sqrt{15}y=0$ |
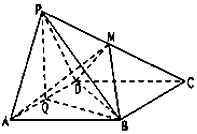 如图,在四棱锥P-ABCD中,底面ABCD为菱形,其中PA=PD=AD=2,∠BAD=60°,Q为AD的中点.
如图,在四棱锥P-ABCD中,底面ABCD为菱形,其中PA=PD=AD=2,∠BAD=60°,Q为AD的中点.