4.已知抛物线x2=4y上一点A纵坐标为4,则点A到抛物线焦点的距离为( )
| A. | $\sqrt{10}$ | B. | 4 | C. | 5 | D. | $\sqrt{15}$ |
19.已知点F2,P分别为双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的右焦点与右支上的一点,O为坐标原点,若2$\overrightarrow{OM}=\overrightarrow{OP}+\overrightarrow{O{F_2}},|{\overrightarrow{O{F_2}}}|=|{\overrightarrow{{F_2}M}}$|,且$\overrightarrow{O{F_2}}•\overrightarrow{{F_2}M}=\frac{c^2}{2}$,则该双曲线的离心率为( )
| A. | $2\sqrt{3}$ | B. | $\frac{3}{2}$ | C. | $\sqrt{3}$ | D. | $\frac{{\sqrt{3}+1}}{2}$ |
18.在平行四边形ABCD中,$|{\overrightarrow{AD}}|=3,|{\overrightarrow{AB}}|=5,\overrightarrow{AE}=\frac{2}{3}\overrightarrow{AD},\overrightarrow{BF}=\frac{1}{3}\overrightarrow{BC},cosA=\frac{3}{5}$,则$|{\overrightarrow{EF}}$|=( )
| A. | $\sqrt{14}$ | B. | $2\sqrt{5}$ | C. | $4\sqrt{2}$ | D. | $2\sqrt{11}$ |
16.某电子产品公司前四年的年宣传费x(单位:千万元)与年销售量y(单位:百万部)的数据如下表所示:
可以求y关于x的线性回归方程为$\stackrel{∧}{y}$=1.9x+1.
(1)该公司下一年准备投入10千万元的宣传费,根据所求得的回归方程预测下一年的销售量m:
(2)根据下表所示五个散点数据,求出y关于x的线性回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$.
并利用小二乘法的原理说明$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$与$\stackrel{∧}{y}$=1.9x+1的关系.
参考公式:回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$中斜率和截距的最小二乘法估计公式分别为:
$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{{\sum_{i=1}^{n}x}_{i}^{2}-n{\overline{x}}^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$.
0 239130 239138 239144 239148 239154 239156 239160 239166 239168 239174 239180 239184 239186 239190 239196 239198 239204 239208 239210 239214 239216 239220 239222 239224 239225 239226 239228 239229 239230 239232 239234 239238 239240 239244 239246 239250 239256 239258 239264 239268 239270 239274 239280 239286 239288 239294 239298 239300 239306 239310 239316 239324 266669
| x(单位:千万元) | 1 | 2 | 3 | 4 |
| y(单位:百万部) | 3 | 5 | 6 | 9 |
(1)该公司下一年准备投入10千万元的宣传费,根据所求得的回归方程预测下一年的销售量m:
(2)根据下表所示五个散点数据,求出y关于x的线性回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$.
| x(单位:千万元) | 1 | 2 | 3 | 4 | 10 |
| y(单位:百万部) | 3 | 5 | 6 | 9 | m |
参考公式:回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$中斜率和截距的最小二乘法估计公式分别为:
$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{{\sum_{i=1}^{n}x}_{i}^{2}-n{\overline{x}}^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$.
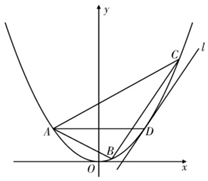 如图,已知A、B、C、D为抛物线E:x2=2py(p>0)上不同四点,其中A、D关于y轴对称,过点D作抛物线E的切线l和直线BC平行.
如图,已知A、B、C、D为抛物线E:x2=2py(p>0)上不同四点,其中A、D关于y轴对称,过点D作抛物线E的切线l和直线BC平行.