题目内容
18.在平行四边形ABCD中,$|{\overrightarrow{AD}}|=3,|{\overrightarrow{AB}}|=5,\overrightarrow{AE}=\frac{2}{3}\overrightarrow{AD},\overrightarrow{BF}=\frac{1}{3}\overrightarrow{BC},cosA=\frac{3}{5}$,则$|{\overrightarrow{EF}}$|=( )| A. | $\sqrt{14}$ | B. | $2\sqrt{5}$ | C. | $4\sqrt{2}$ | D. | $2\sqrt{11}$ |
分析 如图,取AE的中点G,连接BG,由题意可得$\overrightarrow{EF}$=$\overrightarrow{GB}$,再根据向量的三角形法则和向量的模以及向量的数量积公式计算即可.
解答 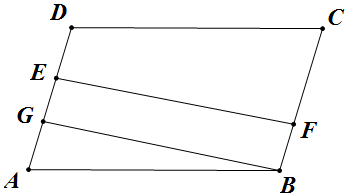 解:如图,取AE的中点G,连接BG
解:如图,取AE的中点G,连接BG
∵$\overrightarrow{AE}$=$\frac{2}{3}$$\overrightarrow{AD}$,$\overrightarrow{BF}$=$\frac{1}{3}$$\overrightarrow{BC}$,
∴$\overrightarrow{AG}$=$\frac{1}{2}$$\overrightarrow{AE}$=$\frac{1}{3}$$\overrightarrow{AD}$=$\frac{1}{3}$$\overrightarrow{BC}$=$\overrightarrow{BF}$,
∴$\overrightarrow{EF}$=$\overrightarrow{GB}$,
∴|$\overrightarrow{GB}$|2=|$\overrightarrow{AB}$-$\overrightarrow{AG}$|2=${\overrightarrow{AB}}^{2}$-2$\overrightarrow{AB}$•$\overrightarrow{AG}$+${\overrightarrow{AG}}^{2}$=52-2×5×1×$\frac{3}{5}$+1=20,
∴|$\overrightarrow{EF}$|=|$\overrightarrow{GB}$|=2$\sqrt{5}$,
故选:B
点评 本题向量的三角形法则和向量的模以及向量的数量积公式,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.在复平面内,复数z的对应点为(1,2),复数z的共轭复数为( )
| A. | 1+2i | B. | 1-2i | C. | -2+i | D. | -2-i |
10.已知双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$(a>0,b>0)过点$(\sqrt{2},2\sqrt{2})$,过点(0,-2)的直线l与双曲线C的一条渐进线平行,且这两条平行线间的距离为$\frac{2}{3}$,则双曲线C的实轴长为( )
| A. | 2 | B. | $2\sqrt{2}$ | C. | 4 | D. | $4\sqrt{2}$ |
7.已知复数z满足(3-i)z=2+i(i为虚数单位),则z的共轭复数是( )
| A. | $\frac{1}{2}$+$\frac{1}{2}$i | B. | $\frac{1}{2}$-$\frac{1}{2}i$ | C. | -$\frac{1}{2}$+$\frac{1}{2}$i | D. | -$\frac{1}{2}$-$\frac{1}{2}$i |
8.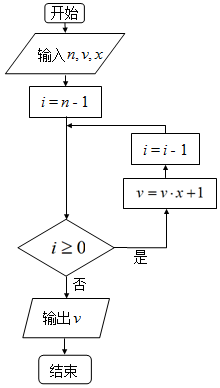 我国南宋时期的数学家秦九韶(约1202-1261)在他的著作《数书九章》中提出了多项式求值的秦九韶算法.如图所示的框图给出了利用秦九韶算法求多项式的一个实例.若输入的n=5,v=1,x=2,则程序框图计算的是( )
我国南宋时期的数学家秦九韶(约1202-1261)在他的著作《数书九章》中提出了多项式求值的秦九韶算法.如图所示的框图给出了利用秦九韶算法求多项式的一个实例.若输入的n=5,v=1,x=2,则程序框图计算的是( )
 我国南宋时期的数学家秦九韶(约1202-1261)在他的著作《数书九章》中提出了多项式求值的秦九韶算法.如图所示的框图给出了利用秦九韶算法求多项式的一个实例.若输入的n=5,v=1,x=2,则程序框图计算的是( )
我国南宋时期的数学家秦九韶(约1202-1261)在他的著作《数书九章》中提出了多项式求值的秦九韶算法.如图所示的框图给出了利用秦九韶算法求多项式的一个实例.若输入的n=5,v=1,x=2,则程序框图计算的是( )| A. | 25+24+23+22+2+1 | B. | 25+24+23+22+2+5 | ||
| C. | 26+25+24+23+22+2+1 | D. | 24+23+22+2+1 |
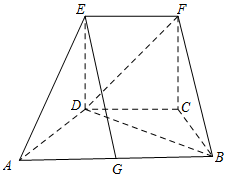 如图所示的几何体中,四边形ABCD为等腰梯形,AB∥CD,AB=2AD=2,∠DAB=60°,四边形CDEF为正方形,平面CDEF⊥平面ABCD.
如图所示的几何体中,四边形ABCD为等腰梯形,AB∥CD,AB=2AD=2,∠DAB=60°,四边形CDEF为正方形,平面CDEF⊥平面ABCD.