题目内容
2.巳知函数f(x)是定义在R上的奇函数,且当x∈(0,+∞)时,都有不等式f(x)+xf'(x)>0成立,若$a={4^{0.2}}f({{4^{0.2}}}),b=({{{log}_4}3})f({{{log}_4}3}),c=({{{log}_4}\frac{1}{16}})f({{{log}_4}\frac{1}{16}})$,则a,b,c的大小关系是c>a>b.分析 根据题意,令g(x)=xf(x),则a=g(40.2),b=g(log43),c=f(log4$\frac{1}{16}$),由函数的奇偶性定义分析可得g(x)为偶函数,对g(x)求导可得g′(x)>0,即g(x)在(0,+∞)上为增函数,比较可得|log4$\frac{1}{16}$|>|40.2|>|log43|,结合函数的单调性分析可得答案.
解答 解:根据题意,令g(x)=xf(x),则a=g(40.2),b=g(log43),c=f(log4$\frac{1}{16}$)
有g(-x)=(-x)f(-x)=(-x)[-f(x)]=xf(x),则g(x)为偶函数,
又由g′(x)=(x)′f(x)+xf'(x)=f(x)+xf'(x),
又由当x∈(0,+∞)时,都有不等式f(x)+xf'(x)>0成立,
则当x∈(0,+∞)时,有g′(x)>0,即g(x)在(0,+∞)上为增函数,
分析可得|log4$\frac{1}{16}$|>|40.2|>|log43|,
则有c>a>b;
故答案为:c>a>b.
点评 本题考查函数的导数与单调性的关系,涉及函数奇偶性的性质应用,关键是构造函数g(x)=xf(x).

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案
相关题目
10.某单位员工按年龄分为A,B,C三组,其人数之比为5:4:1,现用分层抽样的方法从总体中抽取一个容量为10的样本,已知C组中某个员工被抽到的概率是$\frac{1}{9}$,则该单位员工总数为( )
| A. | 110 | B. | 10 | C. | 90 | D. | 80 |
14.若f(x)为奇函数,且x0是y=f(x)-ex的一个零点,则下列函数中,-x0一定是其零点的函数是( )
| A. | y=f(-x)•e-x-1 | B. | y=f(x)•ex+1 | C. | y=f(x)•ex-1 | D. | y=f(-x)•ex+1 |
11.已知数列{an}是等比数列,a1=$\frac{\sqrt{2}}{2}$,a4=2,则a1+a2+…+a10等于( )
| A. | $\frac{31\sqrt{2}}{2}$+31 | B. | 31$\sqrt{2}$+31 | C. | 80 | D. | $\frac{5\sqrt{2}}{2}$+80 |
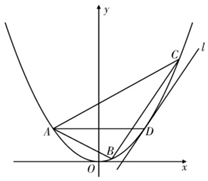 如图,已知A、B、C、D为抛物线E:x2=2py(p>0)上不同四点,其中A、D关于y轴对称,过点D作抛物线E的切线l和直线BC平行.
如图,已知A、B、C、D为抛物线E:x2=2py(p>0)上不同四点,其中A、D关于y轴对称,过点D作抛物线E的切线l和直线BC平行.