题目内容
20.已知$a=\int_0^π{2sin\frac{x}{2}}cos\frac{x}{2}dx$,则a=2.分析 先化简被积函数,再根据定积分的计算法则计算即可.
解答 解:$a=\int_0^π{2sin\frac{x}{2}}cos\frac{x}{2}dx$=${∫}_{0}^{π}$sinxdx=-cosx|${\;}_{0}^{π}$=-(cosπ-cos0)=2,
故答案为:2
点评 本题考查了定积分的计算和三角函数的化简,属于基础题.

练习册系列答案
相关题目
11.下列函数中,既是偶函数又是(0,+∞)上的增函数的是( )
| A. | y=x3 | B. | y=2|x| | C. | y=-x2 | D. | y=log3(-x) |
8.已知双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的一条渐近线与直线l:x-y+2=0平行,则双曲线C的离心率为( )
| A. | $\frac{\sqrt{5}}{2}$ | B. | $\sqrt{2}$ | C. | $\frac{2\sqrt{3}}{3}$ | D. | $\sqrt{10}$ |
5.已知点F2,P分别为双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的右焦点与右支上的一点,O为坐标原点,若点M是PF2的中点,$|{\overrightarrow{O{F_2}}}|=|{\overrightarrow{{F_2}M}}$|,且$\overrightarrow{O{F_2}}•\overrightarrow{{F_2}M}=\frac{c^2}{2}$,则该双曲线的离心率为( )
| A. | $\frac{{\sqrt{3}+1}}{2}$ | B. | $\frac{3}{2}$ | C. | $\sqrt{3}$ | D. | $2\sqrt{3}$ |
9.(1-$\sqrt{x}$)6(1-$\root{3}{x}$)4的展开式中,x2的系数是( )
| A. | -75 | B. | -45 | C. | 45 | D. | 75 |
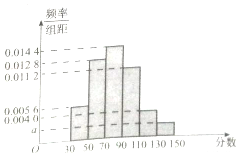 某市高二年级学生进行数学竞赛,竞赛分为初赛和决赛,规定成绩在110分及110分以上的学生进入决赛,110分以下的学生则被淘汰,现随机抽取500名学生的初赛成绩按[30,50),[50,70),[70,90),[90,110),[110,130),[130,150]做成频率副本直方图,如图所示:(假设成绩在频率分布直方图中各段是均匀分布的)
某市高二年级学生进行数学竞赛,竞赛分为初赛和决赛,规定成绩在110分及110分以上的学生进入决赛,110分以下的学生则被淘汰,现随机抽取500名学生的初赛成绩按[30,50),[50,70),[70,90),[90,110),[110,130),[130,150]做成频率副本直方图,如图所示:(假设成绩在频率分布直方图中各段是均匀分布的)