题目内容
4.已知抛物线x2=4y上一点A纵坐标为4,则点A到抛物线焦点的距离为( )| A. | $\sqrt{10}$ | B. | 4 | C. | 5 | D. | $\sqrt{15}$ |
分析 先根据抛物线的方程求得准线的方程,进而利用点A的纵坐标求得点A到准线的距离,进而根据抛物线的定义求得答案.
解答 解:依题意可知抛物线的准线方程为y=-1,
∴点A到准线的距离为4+1=5,
根据抛物线的定义可知点A与抛物线焦点的距离就是点A与抛物线准线的距离,
∴点A与抛物线焦点的距离为5,
故选:C.
点评 本题主要考查了抛物线的定义的运用.考查了学生对抛物线基础知识的掌握.属基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
12.已知函数f(x)的导函数f′(x),满足(x-1)[xf′(x)-f(x)]>0,则下列关于f(x)的命题正确的是( )
| A. | f(3)<f(-3) | B. | f(2)>f(-2) | C. | f(3)<f(2) | D. | 2f(3)>3f(2) |
19.已知点F2,P分别为双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的右焦点与右支上的一点,O为坐标原点,若2$\overrightarrow{OM}=\overrightarrow{OP}+\overrightarrow{O{F_2}},|{\overrightarrow{O{F_2}}}|=|{\overrightarrow{{F_2}M}}$|,且$\overrightarrow{O{F_2}}•\overrightarrow{{F_2}M}=\frac{c^2}{2}$,则该双曲线的离心率为( )
| A. | $2\sqrt{3}$ | B. | $\frac{3}{2}$ | C. | $\sqrt{3}$ | D. | $\frac{{\sqrt{3}+1}}{2}$ |
9.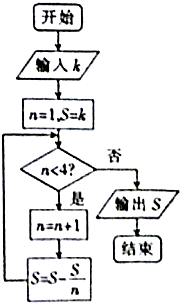 我国古代数学著作《九章算术》有如下问题:“今有器中米,不知其数,前人取半,中人三分取一,后人四分取一,余米一斗五升.问,米几何?”如图是解决该问题的程序框图,执行该程序框图,若输出的S=1.5(单位:升),则输入k的值为( )
我国古代数学著作《九章算术》有如下问题:“今有器中米,不知其数,前人取半,中人三分取一,后人四分取一,余米一斗五升.问,米几何?”如图是解决该问题的程序框图,执行该程序框图,若输出的S=1.5(单位:升),则输入k的值为( )
 我国古代数学著作《九章算术》有如下问题:“今有器中米,不知其数,前人取半,中人三分取一,后人四分取一,余米一斗五升.问,米几何?”如图是解决该问题的程序框图,执行该程序框图,若输出的S=1.5(单位:升),则输入k的值为( )
我国古代数学著作《九章算术》有如下问题:“今有器中米,不知其数,前人取半,中人三分取一,后人四分取一,余米一斗五升.问,米几何?”如图是解决该问题的程序框图,执行该程序框图,若输出的S=1.5(单位:升),则输入k的值为( )| A. | 4.5 | B. | 6 | C. | 7.5 | D. | 9 |
13.已知实数x,y满足$\left\{\begin{array}{l}{3x-y-7≥0}\\{5x-4y≤0}\\{y≤10}\end{array}\right.$,则$\frac{y+x}{x}$的最大值为( )
| A. | 1 | B. | $\frac{30}{17}$ | C. | $\frac{47}{17}$ | D. | 2 |
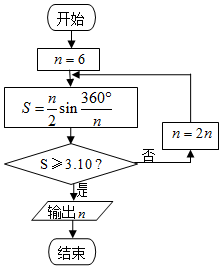 公元263年左右,我国古代数学家刘徽用圆内接正多边形的面积去逼近圆的面积求圆周率π,刘徽称这个方法为“割圆术”,并且把“割圆术”的特点概括为“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣”下图是根据刘徽的“割圆术”思想设计的一个程序框图.若运行该程序,则输出的n的值为:(参考数据:$\sqrt{3}$≈1.732,sin15°≈0.2588,sin7.5°≈0.1305)( )
公元263年左右,我国古代数学家刘徽用圆内接正多边形的面积去逼近圆的面积求圆周率π,刘徽称这个方法为“割圆术”,并且把“割圆术”的特点概括为“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣”下图是根据刘徽的“割圆术”思想设计的一个程序框图.若运行该程序,则输出的n的值为:(参考数据:$\sqrt{3}$≈1.732,sin15°≈0.2588,sin7.5°≈0.1305)( )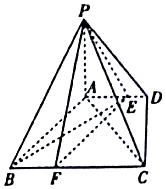 如图,四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD是直角梯形,∠ADC=90°,AD∥BC,AB⊥AC,AB=AC=$\sqrt{2}$,点E在AD上,且AE=2ED.
如图,四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD是直角梯形,∠ADC=90°,AD∥BC,AB⊥AC,AB=AC=$\sqrt{2}$,点E在AD上,且AE=2ED.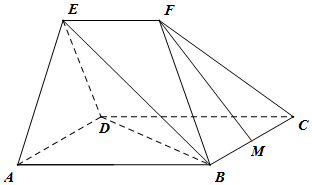 如图,在几何体ABCDEF中,平面ADE⊥平面ABCD,四边形ABCD为菱形,且∠DAB=60°,EA=ED=AB=2EF,EF∥AB,M为BC中点.
如图,在几何体ABCDEF中,平面ADE⊥平面ABCD,四边形ABCD为菱形,且∠DAB=60°,EA=ED=AB=2EF,EF∥AB,M为BC中点.