12.已知函数f(x)的导函数f′(x),满足(x-1)[xf′(x)-f(x)]>0,则下列关于f(x)的命题正确的是( )
| A. | f(3)<f(-3) | B. | f(2)>f(-2) | C. | f(3)<f(2) | D. | 2f(3)>3f(2) |
11.已知三棱锥P-ABC的各顶点都在同一球的面上,且PA⊥平面ABC,若球O的体积为$\frac{20\sqrt{5}π}{3}$(球的体积公式:V=$\frac{4π}{3}$R3,其中R为球的半径),AB=2,AC=1,∠BAC=60°,则PA为( )
| A. | 4 | B. | $\sqrt{5}$ | C. | 2 | D. | $\sqrt{3}$ |
10.某单位员工按年龄分为A,B,C三组,其人数之比为5:4:1,现用分层抽样的方法从总体中抽取一个容量为10的样本,已知C组中某个员工被抽到的概率是$\frac{1}{9}$,则该单位员工总数为( )
| A. | 110 | B. | 10 | C. | 90 | D. | 80 |
9.牛顿法求方程f(x)=0近似根原理如下:求函数y=f(x)在点(xn,f(xn))处的切线y=f′(xn)(x-xn)+f(xn),其与x轴交点横坐标xn+1=xn-$\frac{f({x}_{n})}{f′({x}_{n})}$(n∈N*),则xn+1比xn更靠近f(x)=0的根,现已知f(x)=x2-3,求f(x)=0的一个根的程序框图如图所示,则输出的结果为( )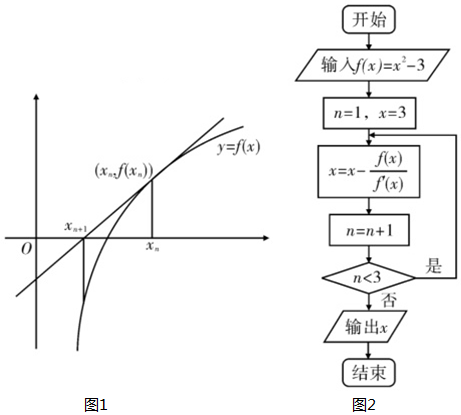

| A. | 2 | B. | 1.75 | C. | 1.732 | D. | 1.73 |
8.已知双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的一条渐近线与直线l:x-y+2=0平行,则双曲线C的离心率为( )
| A. | $\frac{\sqrt{5}}{2}$ | B. | $\sqrt{2}$ | C. | $\frac{2\sqrt{3}}{3}$ | D. | $\sqrt{10}$ |
7.已知向量$\overrightarrow{m}$=(-1,1),$\overrightarrow{n}$=(t,2),若$\overrightarrow{m}$⊥$\overrightarrow{n}$,则|$\overrightarrow{m}$+$\overrightarrow{n}$|=( )
| A. | 2$\sqrt{2}$ | B. | $\sqrt{5}$ | C. | 2$\sqrt{3}$ | D. | $\sqrt{10}$ |
6.在复平面内,复数z的对应点为(1,2),复数z的共轭复数为( )
0 239129 239137 239143 239147 239153 239155 239159 239165 239167 239173 239179 239183 239185 239189 239195 239197 239203 239207 239209 239213 239215 239219 239221 239223 239224 239225 239227 239228 239229 239231 239233 239237 239239 239243 239245 239249 239255 239257 239263 239267 239269 239273 239279 239285 239287 239293 239297 239299 239305 239309 239315 239323 266669
| A. | 1+2i | B. | 1-2i | C. | -2+i | D. | -2-i |