题目内容
7.已知向量$\overrightarrow{m}$=(-1,1),$\overrightarrow{n}$=(t,2),若$\overrightarrow{m}$⊥$\overrightarrow{n}$,则|$\overrightarrow{m}$+$\overrightarrow{n}$|=( )| A. | 2$\sqrt{2}$ | B. | $\sqrt{5}$ | C. | 2$\sqrt{3}$ | D. | $\sqrt{10}$ |
分析 根据向量的垂直关系求出t的值,求出$\overrightarrow{m}$+$\overrightarrow{n}$的坐标,从而求出$\overrightarrow{m}$+$\overrightarrow{n}$的模即可.
解答 解:$\overrightarrow{m}$=(-1,1),$\overrightarrow{n}$=(t,2),
若$\overrightarrow{m}$⊥$\overrightarrow{n}$,则2-t=0,解得:t=2,
故:$\overrightarrow{m}$=(-1,1),$\overrightarrow{n}$=(2,2),
$\overrightarrow{m}$+$\overrightarrow{n}$=(1,3),
故|$\overrightarrow{m}$+$\overrightarrow{n}$|=$\sqrt{1+9}$=$\sqrt{10}$,
故选:D.
点评 本题考查向量垂直的条件:数量积为0,考查向量求模问题,是一道基础题.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
2.已知函数f(x)为偶函数,当x≤0时,f(x)为增函数,则“$\frac{6}{5}$<x<2”是“f[log2(2x-2)]>f(log${\;}_{\frac{1}{2}}$$\frac{2}{3}$)”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
12.已知函数f(x)的导函数f′(x),满足(x-1)[xf′(x)-f(x)]>0,则下列关于f(x)的命题正确的是( )
| A. | f(3)<f(-3) | B. | f(2)>f(-2) | C. | f(3)<f(2) | D. | 2f(3)>3f(2) |
19.已知点F2,P分别为双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的右焦点与右支上的一点,O为坐标原点,若2$\overrightarrow{OM}=\overrightarrow{OP}+\overrightarrow{O{F_2}},|{\overrightarrow{O{F_2}}}|=|{\overrightarrow{{F_2}M}}$|,且$\overrightarrow{O{F_2}}•\overrightarrow{{F_2}M}=\frac{c^2}{2}$,则该双曲线的离心率为( )
| A. | $2\sqrt{3}$ | B. | $\frac{3}{2}$ | C. | $\sqrt{3}$ | D. | $\frac{{\sqrt{3}+1}}{2}$ |
17.已知函数$f(x)=sin(ωx+\frac{π}{6})(ω>0)$的最小正周期为4π,则( )
| A. | 函数f(x)的图象关于原点对称 | |
| B. | 函数f(x)的图象关于直线$x=\frac{π}{3}$对称 | |
| C. | 函数f(x)图象上的所有点向右平移$\frac{π}{3}$个单位长度后,所得的图象关于原点对称 | |
| D. | 函数f(x)在区间(0,π)上单调递增 |
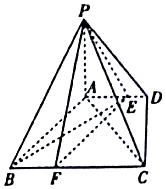 如图,四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD是直角梯形,∠ADC=90°,AD∥BC,AB⊥AC,AB=AC=$\sqrt{2}$,点E在AD上,且AE=2ED.
如图,四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD是直角梯形,∠ADC=90°,AD∥BC,AB⊥AC,AB=AC=$\sqrt{2}$,点E在AD上,且AE=2ED.