题目内容
9.牛顿法求方程f(x)=0近似根原理如下:求函数y=f(x)在点(xn,f(xn))处的切线y=f′(xn)(x-xn)+f(xn),其与x轴交点横坐标xn+1=xn-$\frac{f({x}_{n})}{f′({x}_{n})}$(n∈N*),则xn+1比xn更靠近f(x)=0的根,现已知f(x)=x2-3,求f(x)=0的一个根的程序框图如图所示,则输出的结果为( )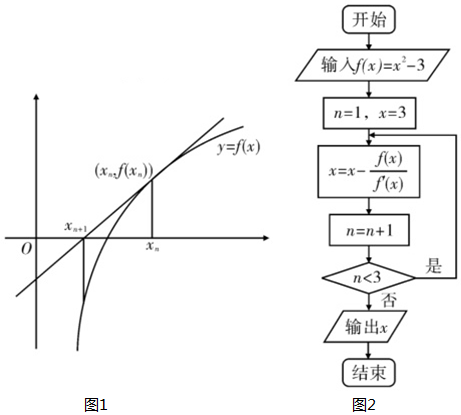
| A. | 2 | B. | 1.75 | C. | 1.732 | D. | 1.73 |
分析 模拟程序的运行,依次写出每次循环得到的x,n的值,当n=3时不满足条件n<3,退出循环,输出x的值为$\frac{7}{4}$,即可得解.
解答 解:f(x)=x2-3,则f′(x)=2x,
模拟程序的运行,可得
n=1,x=3
执行循环体,x=3-$\frac{6}{6}$=2,n=2
满足条件n<3,执行循环体,x=2-$\frac{1}{4}$=$\frac{7}{4}$,n=3
不满足条件n<3,退出循环,输出x的值为$\frac{7}{4}$,即1.75.
故选:B.
点评 本题主要考查了循环结构的程序框图,模拟程序的运行是解决此类问题的一般方法,属于基础题.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
19.某经销商从外地一水殖厂购进一批小龙虾,并随机抽取40只进行统计,按重量分类统计结果如下图:
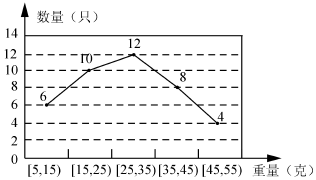
(1)记事件A为:“从这批小龙虾中任取一只,重量不超过35g的小龙虾”,求P(A)的估计值;
(2)试估计这批小龙虾的平均重量;
(3)为适应市场需求,制定促销策略.该经销商又将这批小龙虾分成三个等级,并制定出销售单价,如下表:
试估算该经销商以每千克至多花多少元(取整数)收购这批小龙虾,才能获得利润?

(1)记事件A为:“从这批小龙虾中任取一只,重量不超过35g的小龙虾”,求P(A)的估计值;
(2)试估计这批小龙虾的平均重量;
(3)为适应市场需求,制定促销策略.该经销商又将这批小龙虾分成三个等级,并制定出销售单价,如下表:
| 等级 | 一等品 | 二等品 | 三等品 |
| 重量(g) | [5,25) | [25,35) | [35,55] |
| 单价(元/只) | 1.2 | 1.5 | 1.8 |
19.已知i为虚数单位,则复数z=(1+i)i对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |