题目内容
11.已知三棱锥P-ABC的各顶点都在同一球的面上,且PA⊥平面ABC,若球O的体积为$\frac{20\sqrt{5}π}{3}$(球的体积公式:V=$\frac{4π}{3}$R3,其中R为球的半径),AB=2,AC=1,∠BAC=60°,则PA为( )| A. | 4 | B. | $\sqrt{5}$ | C. | 2 | D. | $\sqrt{3}$ |
分析 利用球的体积,求出球的半径,利用余弦定理求出BC,可得△ABC外接圆的半径,利用勾股定理可得结论.
解答 解:球O的体积为$\frac{20\sqrt{5}π}{3}$,$\frac{4π}{3}$R3=$\frac{20\sqrt{5}π}{3}$,∴R=$\sqrt{5}$.
∵AB=2,AC=1,∠BAC=60°,
∴BC=$\sqrt{4+1-2×2×1×\frac{1}{2}}$=$\sqrt{3}$,
∴△ABC外接圆的半径为$\frac{1}{2}×\frac{\sqrt{3}}{\frac{\sqrt{3}}{2}}$=1,
∴$\sqrt{1+\frac{1}{4}P{A}^{2}}$=$\sqrt{5}$,∴PA=4,
故选A.
点评 本题考查球的体积,余弦定理,考查学生的计算能力,属于中档题.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案
相关题目
2.下列函数中,既是偶函数又是(0,+∞)上的增函数的是( )
| A. | y=-x3 | B. | y=2|x| | C. | y=${x}^{\frac{1}{2}}$ | D. | y=log3(-x) |
6.在复平面内,复数z的对应点为(1,2),复数z的共轭复数为( )
| A. | 1+2i | B. | 1-2i | C. | -2+i | D. | -2-i |
16.某电子产品公司前四年的年宣传费x(单位:千万元)与年销售量y(单位:百万部)的数据如下表所示:
可以求y关于x的线性回归方程为$\stackrel{∧}{y}$=1.9x+1.
(1)该公司下一年准备投入10千万元的宣传费,根据所求得的回归方程预测下一年的销售量m:
(2)根据下表所示五个散点数据,求出y关于x的线性回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$.
并利用小二乘法的原理说明$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$与$\stackrel{∧}{y}$=1.9x+1的关系.
参考公式:回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$中斜率和截距的最小二乘法估计公式分别为:
$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{{\sum_{i=1}^{n}x}_{i}^{2}-n{\overline{x}}^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$.
| x(单位:千万元) | 1 | 2 | 3 | 4 |
| y(单位:百万部) | 3 | 5 | 6 | 9 |
(1)该公司下一年准备投入10千万元的宣传费,根据所求得的回归方程预测下一年的销售量m:
(2)根据下表所示五个散点数据,求出y关于x的线性回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$.
| x(单位:千万元) | 1 | 2 | 3 | 4 | 10 |
| y(单位:百万部) | 3 | 5 | 6 | 9 | m |
参考公式:回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$中斜率和截距的最小二乘法估计公式分别为:
$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{{\sum_{i=1}^{n}x}_{i}^{2}-n{\overline{x}}^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$.
1. 执行如图所示的程序框图,则输出的S值是( )
执行如图所示的程序框图,则输出的S值是( )
 执行如图所示的程序框图,则输出的S值是( )
执行如图所示的程序框图,则输出的S值是( )| A. | 15 | B. | 29 | C. | 31 | D. | 63 |
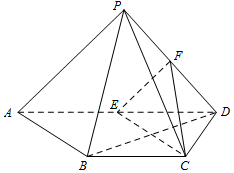 如图,四棱锥P-ABCD中,PD⊥平面PAB,AD∥BC,BC=CD=$\frac{1}{2}$AD,E,F分别为线段AD,PD的中点.
如图,四棱锥P-ABCD中,PD⊥平面PAB,AD∥BC,BC=CD=$\frac{1}{2}$AD,E,F分别为线段AD,PD的中点.