1.对函数f(x),在使f(x)≥M成立的所有常数M中,我们把M的最大值叫做函数f(x)的下确界.现已知定义在R上的偶函数f(x)满足f(1-x)=f(1+x),当x∈[0,1]时,f(x)=-3x2+2,则f(x)的下确界为( )
| A. | 2 | B. | 1 | C. | -2 | D. | -1 |
20.已知F1、F2分别是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$的左、右焦点,P为双曲线右支上的任意一点且$\frac{|P{F}_{1}{|}^{2}}{|P{F}_{2}|}$=8a,则双曲线离心率的取值范围是( )
| A. | (1,3] | B. | [3,+∞) | C. | (1,2] | D. | [2,+∞) |
17.将函数$f(x)=3sin(2x+\frac{π}{3})$的图象向左平移$\frac{π}{6}$个单位,在向上平移1个单位,得到g(x)的图象,若g(x1)g(2)=16,且${x_1},{x_2}∈[-\frac{3π}{2},\frac{3π}{2}]$,则2x1-x2的最大值为( )
| A. | $\frac{23}{12}π$ | B. | $\frac{35}{12}π$ | C. | $\frac{19}{6}π$ | D. | $\frac{59}{12}π$ |
16.已知三棱锥S-ABC的各顶点都在一个球面上,△ABC所在截面圆的圆心O在AB上,SO⊥平面$ABC,AC=\sqrt{3},BC=1$,若三棱锥的体积是$\frac{{\sqrt{3}}}{3}$,则球体的表面积是( )
0 239110 239118 239124 239128 239134 239136 239140 239146 239148 239154 239160 239164 239166 239170 239176 239178 239184 239188 239190 239194 239196 239200 239202 239204 239205 239206 239208 239209 239210 239212 239214 239218 239220 239224 239226 239230 239236 239238 239244 239248 239250 239254 239260 239266 239268 239274 239278 239280 239286 239290 239296 239304 266669
| A. | $\frac{25}{4}π$ | B. | $\frac{25}{12}π$ | C. | $\frac{125}{48}π$ | D. | 25π |
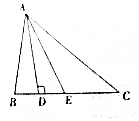 如图,在△ABC中,AD是BC上的高,AE平分∠BAC,∠B=75°,∠C=45°,求∠DAE与∠AEC的度数.
如图,在△ABC中,AD是BC上的高,AE平分∠BAC,∠B=75°,∠C=45°,求∠DAE与∠AEC的度数.