题目内容
1.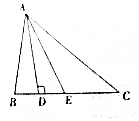 如图,在△ABC中,AD是BC上的高,AE平分∠BAC,∠B=75°,∠C=45°,求∠DAE与∠AEC的度数.
如图,在△ABC中,AD是BC上的高,AE平分∠BAC,∠B=75°,∠C=45°,求∠DAE与∠AEC的度数.
分析 由∠B=75°,∠C=45°,利用三角形内角和求出∠BAC.又AE平分∠BAC,求出∠BAE、∠CAE.再利用AD是BC上的高在△ABD中求出∠BAD,此时就可以求出∠DAE.最后利用三角形的外角和内角的关系可以求出∠AEC.
解答 解:∵∠B+∠C+∠BAC=180°,∠B=75°,∠C=45°,
∴∠BAC=60°,
∵AE平分∠BAC,
∴∠BAE=∠CAE=$\frac{1}{2}$∠BAC=$\frac{1}{2}$×60°=30°,
∵AD是BC上的高,
∴∠B+∠BAD=90°,
∴∠BAD=90°-∠B=90°-75°=15°,
∴∠DAE=∠BAE-∠BAD=30°-15°=15°,
在△AEC中,∠AEC=180°-∠C-∠CAE=180°-45°-30°=105°.
点评 此题主要考查了三角形的内角,外角以及和它们相关的一些结论,图形比较复杂,对于学生的视图能力要求比较高.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
10.如图所示,向量$\overrightarrow{O{Z_1}},\overrightarrow{O{Z_2}}$所对应的复数分别为Z1,Z2,则Z1•Z2=( )
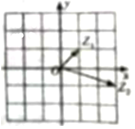

| A. | 4+2i | B. | 2+i | C. | 2+2i | D. | 3+i |
17.将函数$f(x)=3sin(2x+\frac{π}{3})$的图象向左平移$\frac{π}{6}$个单位,在向上平移1个单位,得到g(x)的图象,若g(x1)g(2)=16,且${x_1},{x_2}∈[-\frac{3π}{2},\frac{3π}{2}]$,则2x1-x2的最大值为( )
| A. | $\frac{23}{12}π$ | B. | $\frac{35}{12}π$ | C. | $\frac{19}{6}π$ | D. | $\frac{59}{12}π$ |
11.设集合M={x|(x-1)(x+2)<0},N={x∈Z||x|≤2},则M∩N=( )
| A. | {-1,0} | B. | {0,1} | C. | {-1,0,1} | D. | {0,1,2} |